Advertisements
Advertisements
प्रश्न
Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
उत्तर

Consider the given figure in which l is a line drawn through the mid-point P of line segment AB meeting AC at Q, such that PQ || BC
By using basic proportionality theorem, we obtain
`(AQ)/(QC) = (AP)/(PB)`
`(AQ)/(QC) = 1/1` (P is the midpoint of AB ∴ AP = PB)
⇒ AQ = QC
Or, Q is the mid-point of AC.
APPEARS IN
संबंधित प्रश्न
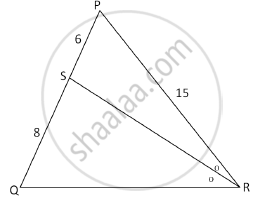
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In figure, find ∠L

In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.

Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
In the given figure, AB and DE are perpendicular to BC.

1) Prove that ΔABC ∼ ΔDEC
2) If AB = 6 cm; DE = 4 cm and AC = 15 cm. Calculate CD.
3) Find the ratio of area of ΔABC: area of ΔDEC
In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC

State, true or false:
Two isosceles-right triangles are similar.
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
A model of a ship if made to a scale of 1 : 200.
(i) Thelength of the model is 4 m; calculate the length of the ship.
(ii) The area of the deck of the ship is 160000 m2; find the area of the deck of the model.
(iii) The volume of the model is 200 litres; calculate the volume of the ship in m3.
In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD

ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1cm, PB = 3cm, AQ = 1.5cm, QC = 4.5cm, prove that area of ΔAPQ is 116 of the area of ΔABC.
∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE?

In Δ ABC , MN || BC .

If `"AB"/"AM" = 9/4` , find `("Ar" ("trapezium MBCN"))/("Ar" . (triangle "ABC"))`
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

In the figure , ABCD is a quadrilateral . F is a point on AD such that AF = 2.1 cm and FD = 4.9 cm . E and G are points on AC and AB respectively such that EF || CD and GE || BC . Find `("Ar" triangle "BCD")/("Ar" triangle "GEF")`

A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.

Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that ΔPTQ - DRTS
Given is a triangle with sides 3 cm, 5 cm and 6 cm. Find the sides of a triangle which is similar to the given triangle and its shortest side is 4.5 cm.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The area on the map that represented the plot of land.
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

If BD ⊥ AC and CE ⊥ AB, prove that ∆AEC ~ ∆ADB

In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
From the given figure, prove that ΔABC ~ ΔEDF
Two similar triangles will always have ________ angles
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
In the figure, which of the following statements is true?
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.

Are triangles in figure similar? If yes, then write the test of similarity.
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
In the given figure, ΔABC ∼ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; them the value of x is ______.

In ΔABC, PQ || BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

