Advertisements
Advertisements
प्रश्न
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Mid point of AE is ______
उत्तर
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Midpoint of AE is C
Explanation:
∵ AB + BC = CD + DE
⇒ AC = CE
APPEARS IN
संबंधित प्रश्न
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AC + ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Midpoint of CE is ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AE = ______ × AB.
The number of common points in the two angles marked in figure is ______.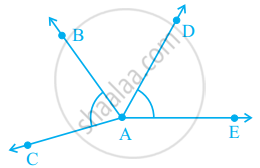
The number of common points in the two angles marked in figure is ______.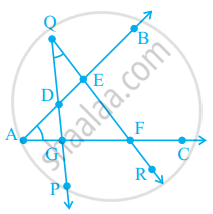
In given figure, is AC + CB = AB ?
In given figure, is AB + AC = CB?
In given figure, is AB + BC = CA?
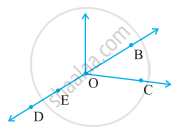
Use the figure to name Five points.
Consider the following figure of line \[\overleftrightarrow{MN}\]. Say whether the following statement is true or false in the context of the given figure.
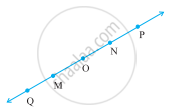
N is the initial point of `vec("NP")` and `vec("NM")`.
