Advertisements
Advertisements
प्रश्न
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Mid point of AE is ______
उत्तर
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Midpoint of AE is C
Explanation:
∵ AB + BC = CD + DE
⇒ AC = CE
APPEARS IN
संबंधित प्रश्न
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AB + ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AC + ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Midpoint of CE is ______
The number of common points in the two angles marked in figure ______.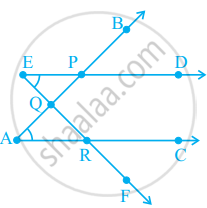
The number of common points in the two angles marked in figure is ______.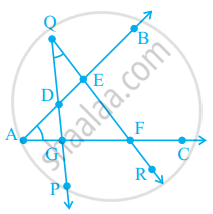
In given figure, is AB + BC = CA?
How many points are marked in the figure?
In the given figure, how many points are marked? Name them.
In given figure, how many points are marked? Name them.
Consider the following figure of line \[\overleftrightarrow{MN}\]. Say whether the following statement is true or false in the context of the given figure.
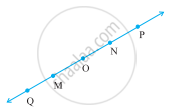
O is not an initial point of `vec("OP")`.
