Advertisements
Advertisements
प्रश्न
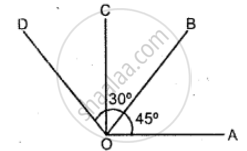
In the given figure:
(i) If ∠AOB = 45°, ∠BOC = 30° and ∠AOD= 110°; find : angles COD and BOD.
(ii) If ∠BOC = ∠DOC = 34° and ∠AOD = 120° ; find : angle AOB and angle AOC.
(iii) If ∠AOB = ∠BOC = ∠COD = 38° find : reflex angle AOC and reflex angle AOD.
उत्तर
(i) ∠COD = ∠AOD – ∠AOC
= ∠AOD – (∠AOB + ∠BOC)
= 110° - (45°+ 30°)
= 110°- 75°
= 35°
∠BOD = ∠AOD -∠AOB
= 110° - 45°
= 65°
(ii) ∠AOB = ∠AOD-∠BOD
= ∠AOD – (∠BOC + ∠COD)
= 120° – (34° + 34°)
= 120°-68°
= 52°
∠AOC = ∠AOB + ∠BOC
= 52° + 34°
= 86°
(iii) Reflex ∠AOC = 360°-∠AOC
= 360° – (∠AOB + ∠BOC)
= 360° – (38° + 38°)
= 360° – 76° = 284°
Reflex ∠AOD = 360° – ∠AOD
= 360° (∠AOB + ∠BOC + ∠COD)
= 360° – (38° + 38° + 38°)
= 360°- 114°
= 246°
APPEARS IN
संबंधित प्रश्न
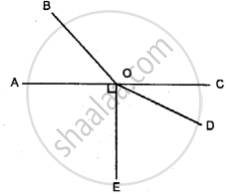
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of:
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.
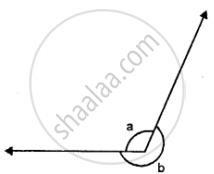
In the given figure if: b = 200 ; find a.
Write the complement angle of: 45°
Write the supplement angle of: 111°
Write the supplement angle of: 20° + y°
`3/4` of 160°
Find the angle that is equal to its supplement?
For an angle x°, find:
(i) the complementary angle
(ii) the supplementary angle
(iii) the value of x° if its supplementary angle is three times its complementary angle.
Explain what do you understand by Adjacent angles?
Two adjacent angles forming a linear pair are in the ratio 7:5, find the angles.
