Advertisements
Advertisements
प्रश्न
निचे दी गई आकृति में किरण AE || किरण BD किरण AF तथा किरण BC क्रमशः ∠ EAB तथा ∠ ABD की समद्विभाजक है तो सिद्ध कीजिए कि रेखा AF || रेखा BC
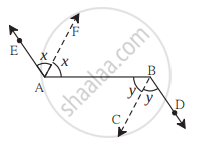
उत्तर
किरण AE || किरण BD ...(दिया है।)
तथा रेखा AB इनकी तिर्यक रेखा है।
∠EAB ≅ ∠ ABD ...(एकांतर कोण)
∴ ∠EAB = ∠ABD
दोनों पक्षों में `1/2` से गुणा करने पर,
`1/2 "∠EAB" = 1/2`∠ABD ...(1)
∠FAB = `1/2` ∠EAB ...(किरण AF, ∠EAB किरण की समद्विभाजक है।) ...(2)
∠ABC = `1/2` ∠ABD ...(किरण BC, ∠ABD किरण की समद्विभाजक है।) ...(3)
∴ ∠FAB = ∠ABC ...[(1), (2), (3) से]
∴ ∠FAB ≅ ∠ABC
∴ रेखा AF || रेखा BC ...(समांतर की एकांतर कोण कसौटी)
APPEARS IN
संबंधित प्रश्न
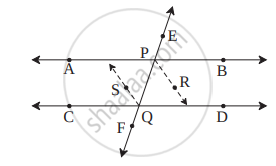
निचे दी गई आकृति में रेखा EF यह रेखा AB तथा रेखा CD को क्रमशः बिंदु P तथा Q पर प्रतिच्छेदित करती है। किरण PR तथा किरण QS परस्पर समांतर किरणें हैं तथा क्रमशः ∠BPQ तथा ∠PQC के समद्विभाजक है, तो सिद्ध कीजिए कि रेखा AB || रेखा CD
निचे दी गई आकृति में रेखा AB || रेखा CF तथा रेखा BC || रेखा ED तो सिद्ध कीजिए कि ∠ABC = ∠FDE.