Advertisements
Advertisements
प्रश्न
Obtain the expression for the energy stored per unit volume in a charged parallel plate capacitor.
उत्तर
Let us consider a parallel-plate capacitor of plate area A
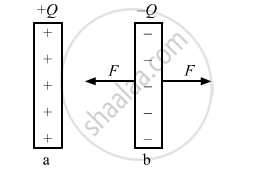
Suppose the plates of the capacitor are almost touching each other and a charge Q is given to the capacitor. One of the plates, say a, is kept fixed and other say b, is slowly pulled away from plate a to increase the separation from zero to d. The attractive force on the plate b at any instant due to first plate is given by:
`F=Q^2/(2Aepsilon_0)`
The person pulling the plate b must apply an equal and opposite force (F) in the opposite direction if the plate is moved slowly.
Work done by the person during the displacement of the second plate:
W = Fd
`=(Q^2d)/(2Aepsilon_0)=Q^2/(2C)`
Here,`C=(Aepsilon_0)/d`, which is the capacitance of the capacitor in the final position.
The work done by the person must be equal to the increase in the energy of the system.
Thus, the capacitor has a stored energy.
`U=Q^2/(2C)`
Now, if we pull the plates of the capacitor apart, we have to do work against the electrostatic attraction between the plates. When we increase the separation between the plates from d1 to d2, an amount `Q^2/(2Aepsilon_0)(d_2-d_1)` of work is performed by us and this much energy goes into the capacitor. On the other hand, new electric field is created in a volume A(d2 - d1).
The energy stored per unit volume is thus given by:
`u=((Q^2(d_2-d_1))/(2Aepsilon_0))/(A(d_2-d_1))=Q^2/(2A^2epsilon_0)`
`1/2epsilon_0(Q/(Aepsilon_0))^2=1/2epsilon_0E^2`
Here, E is the intensity of the electric field.
APPEARS IN
संबंधित प्रश्न
The energy density in the electric field created by a point charge falls off with the distance from the point charge as
A 100 μF capacitor is joined to a 24 V battery through a 1.0 MΩ resistor. Plot qualitative graphs (a) between current and time for the first 10 minutes and (b) between charge and time for the same period.
Two capacitors of capacitances 4⋅0 µF and 6⋅0 µF are connected in series with a battery of 20 V. Find the energy supplied by the battery.
Consider the situation shown in figure. The switch is closed at t = 0 when the capacitors are uncharged. Find the charge on the capacitor C1 as a function of time t.
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
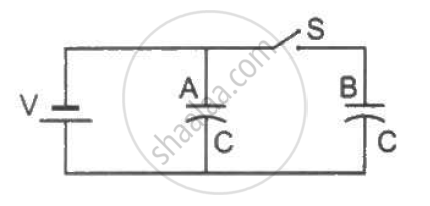
Figure shows two identical parallel plate capacitors connected to a battery through a switch S. Initially, the switch is closed so that the capacitors are completely charged. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant 3. Find the ratio of the initial total energy stored in the capacitors to the final total energy stored.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
A parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is ______
(ε0 = permittivity of free space)
Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.
Electrostatic energy of 4 x 10−4 J is stored in a charged 25 pF capacitor. Find the charge on the capacitor.
