Advertisements
Advertisements
प्रश्न
Obtain the expression for the period of a simple pendulum performing S.H.M.
उत्तर
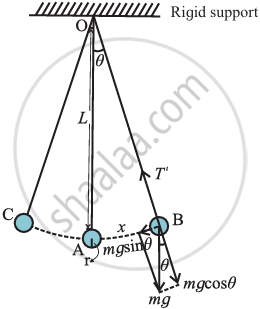
Let m is Mass of the bob.
L is the Length of mass-less string.
A free-body diagram to the forces acting on the bob,
θ − angle made by the string with the vertical.
T is tension along the string
g is the acceleration due to gravity
∴ Restoring force, F = −mg sin θ ...(i)
As θ is very small (θ < 10°), we can write
sin θ ≅ θ° ∴ F ≅ mgθ
From the figure, the small angle `theta = x/L`
∴ `F = -mgx/L` ...(ii)
As m, g and L are constants, F ∝ −x
Thus, for small displacement, the restoring force is directly proportional to the displacement and is oppositely directed.
Hence the bob of a simple pendulum performs linear S.H.M. for small amplitudes. The period T of oscillation of a pendulum from can be given as,
= `(2pi)/omega`
= `(2pi)/sqrt("acceleration per unit displacement")`
Using eq. (ii), `F = -mgx/L`
∴ `a = -gx/L`
∴ `a/x = -g/L = g/L` ...(in magnitude)
Substituting in the expression for T, we get,
`T = 2pi sqrt((L)/(g))` ...(iii)
The equation (iii) gives the expression for the time period of a simple pendulum.
APPEARS IN
संबंधित प्रश्न
A simple pendulum performs S.H.M. of period 4 seconds. How much time after crossing the mean position, will the displacement of the bob be one-third of its amplitude.
A simple pendulum of length 100 cm performs S.H.M. Find the restoring force acting on its bob of mass 50 g when the displacement from the mean position is 3 cm.
In a second’s pendulum, the mass of Bob is 50 g. If it is replaced by 100 g mass, then its period will be ______.
What is a second pendulum?
Obtain an expression for a time period of the simple pendulum.
A simple pendulum of length L has mass m and it oscillates freely with amplitude A. At the extreme position, its potential energy is (g = acceleration due to gravity)
A simple pendulum of length I has a bob of mass m. It executes SHM of small amplitude A. The maximum tension in the string is (g = acceleration due to gravity)
The length of a simple pendulum is increased by 44%. The percentage change in its time period is ______
A simple pendulum has a time period T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of T2 / T1 is ______.
Two pendulums begin to swing simultaneously. The first pendulum makes nine full oscillations when the other makes seven. The ratio of the lengths of the two pendulums is ______.
Two simple pendulums of lengths 1.44 m and 1.96 m start swinging together. After how many vibrations will they again start swinging together?
The length of a seconds pendulum is 1m on the earth. If the mass and diameter of the planet is double than that of the earth, then the length of the second's pendulum on the planet will be ______
A simple pendulum has a length of 2m and a bob of mass of 100 grams. It is whirled in a horizontal plane. If the string breaks under a tension of 10 N, the angle made by the string with vertical is ______
(g = 10 m/s2)
Derive a formula for the length of second's pendulum.
The maximum frequency of transmitted radio waves above which the radio waves are no longer reflected back by ionosphere is ______.
(N = maximum electron density of lonosphere, g = acceleration due to gravity)
The bob of a simple pendulum performs SHM with period T in air and with period T1 in water Relation between T and T1 is ______.
(neglect friction due to water, density of the material of the bob is = `9/8xx10^3` kgm3, density of water = 1 gcc-1)
The ratio of frequencies of two oscillating pendulums is 3 : 2. Their lengths are in the ratio.
A pendulum bob is swinging in a vertical plane, such that its angular amplitude is less than 90°. At its highest point, the string is cut. Which trajectory is possible for bob afterwards?
Two weights w1 and w2 are suspended from the ends of light string over a smooth fixed pulley. If the pulley is pulled up with acceleration g, the tension in the string will be ______.
A simple pendulum of length 196 cm performs linear SHM of amplitude 8 cm. Find the restoring force on its bob of mass 50 g at an extreme position.
A clock regulated by a second pendulum keeps the correct time. During winter the length of the pendulum decreases by 1 %. How much will the clock gain or lose in one day?
