Advertisements
Advertisements
प्रश्न
Obtain the expression for the period of a simple pendulum performing S.H.M.
उत्तर
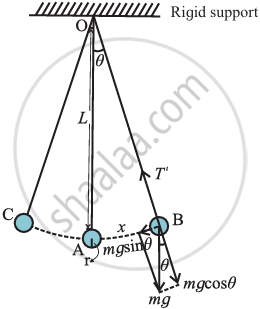
Let m is Mass of the bob.
L is the Length of mass-less string.
A free-body diagram to the forces acting on the bob,
θ − angle made by the string with the vertical.
T is tension along the string
g is the acceleration due to gravity
∴ Restoring force, F = −mg sin θ ...(i)
As θ is very small (θ < 10°), we can write
sin θ ≅ θ° ∴ F ≅ mgθ
From the figure, the small angle `theta = x/L`
∴ `F = -mgx/L` ...(ii)
As m, g and L are constants, F ∝ −x
Thus, for small displacement, the restoring force is directly proportional to the displacement and is oppositely directed.
Hence the bob of a simple pendulum performs linear S.H.M. for small amplitudes. The period T of oscillation of a pendulum from can be given as,
= `(2pi)/omega`
= `(2pi)/sqrt("acceleration per unit displacement")`
Using eq. (ii), `F = -mgx/L`
∴ `a = -gx/L`
∴ `a/x = -g/L = g/L` ...(in magnitude)
Substituting in the expression for T, we get,
`T = 2pi sqrt((L)/(g))` ...(iii)
The equation (iii) gives the expression for the time period of a simple pendulum.
APPEARS IN
संबंधित प्रश्न
Define an ideal simple pendulum.
Answer in brief.
State the law of simple pendulum.
A simple pendulum performs S.H.M. of period 4 seconds. How much time after crossing the mean position, will the displacement of the bob be one-third of its amplitude.
In a second’s pendulum, the mass of Bob is 50 g. If it is replaced by 100 g mass, then its period will be ______.
What is a second pendulum?
A simple pendulum of length L has mass m and it oscillates freely with amplitude A. At the extreme position, its potential energy is (g = acceleration due to gravity)
A simple pendulum of length I has a bob of mass m. It executes SHM of small amplitude A. The maximum tension in the string is (g = acceleration due to gravity)
A bob of a simple pendulum has mass m and is oscillating with an amplitude a. If the length of the pendulum is L, then the maximum tension in the string is [cos 0° = 1, g = acceleration due to gravity]
Work done in stretching a wire through 1 mm is 2 J. What amount of work will be done for elongating another wire of same material, with half the length and double the radius of cross-section, by 1 mm?
Two pendulums begin to swing simultaneously. The first pendulum makes nine full oscillations when the other makes seven. The ratio of the lengths of the two pendulums is ______.
Two light balls are suspended as shown in figure. When a stream of air passes through the space between them, the distance between the balls will ______.
A pendulum performs S.H.M. with period `sqrt3` second in a stationary lift. If lift moves up with acceleration `"g"/3`, the period of pendulum is ______. (g = acceleration due to gravity)
Two simple pendulums of lengths 1.44 m and 1.96 m start swinging together. After how many vibrations will they again start swinging together?
A simple pendulum has a length of 2m and a bob of mass of 100 grams. It is whirled in a horizontal plane. If the string breaks under a tension of 10 N, the angle made by the string with vertical is ______
(g = 10 m/s2)
The maximum kinetic energy of a simple pendulum is 'K'. Its displacement in terms of amplitude 'a', when kinetic energy becomes `(K/2)` is ______.
Derive a formula for the length of second's pendulum.
The maximum frequency of transmitted radio waves above which the radio waves are no longer reflected back by ionosphere is ______.
(N = maximum electron density of lonosphere, g = acceleration due to gravity)
The bob of a simple pendulum performs SHM with period T in air and with period T1 in water Relation between T and T1 is ______.
(neglect friction due to water, density of the material of the bob is = `9/8xx10^3` kgm3, density of water = 1 gcc-1)
The ratio of frequencies of two oscillating pendulums is 3 : 2. Their lengths are in the ratio.
A pendulum bob is swinging in a vertical plane, such that its angular amplitude is less than 90°. At its highest point, the string is cut. Which trajectory is possible for bob afterwards?
Two weights w1 and w2 are suspended from the ends of light string over a smooth fixed pulley. If the pulley is pulled up with acceleration g, the tension in the string will be ______.
A uniform metal rod is used as a bar pendulum. If the room temperature rises by 10°C and coefficient of linear expansion of the metal of the rod is 2 × 106 °C-1, the period of pendulum will increased by ______.
A simple pendulum of length 196 cm performs linear SHM of amplitude 8 cm. Find the restoring force on its bob of mass 50 g at an extreme position.
A clock regulated by a second pendulum keeps the correct time. During winter the length of the pendulum decreases by 1 %. How much will the clock gain or lose in one day?
