Advertisements
Advertisements
प्रश्न
One diagonal of a rectangle is 18 cm. What is the length of its other diagonal?
उत्तर
∵ In a rectangle, diagonals are equal
⇒ AC = BD
Given, one diagonal of a rectangle = 18cm
∴ Other diagonal of a rectangle will be = 18cm
i.e. AC = BD = 18cm.
APPEARS IN
संबंधित प्रश्न
How many diagonals does following have?
A convex quadrilateral
How many diagonals does following have?
A regular hexagon
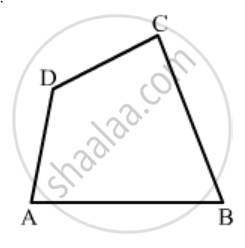
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite angles are there?
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
Complete the following statement by means of one of those given in brackets against each:
If both pairs of opposite sides of a quadrilateral are equal, then it is necessarily a ...............
If ABCD is a rectangle with ∠BAC = 32°, find the measure of ∠DBC.
In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
In parallelogram ABCD, its diagonals intersect at point O. If OA = 6 cm and OB = 7.5 cm, find the length of AC and BD.

ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
A quadrilateral can be drawn when all the four angles and one side is given.
In the given figure.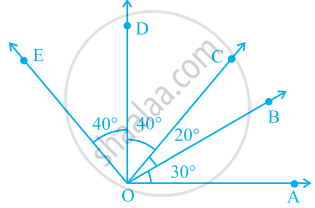
∠AOD is a/an ____ angle
Number of angles less than 180° in figure is ______ and their names are ______.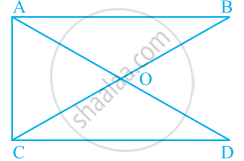
Using the information given, name the right angles in part of figure:
RT ⊥ ST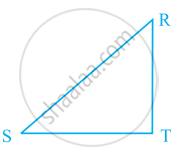
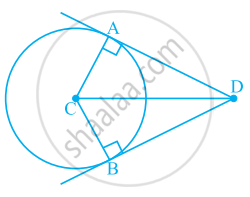
What conclusion can be drawn from part of given figure, if DB is the bisector of ∠ADC?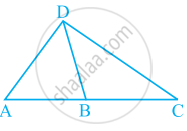
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?