Advertisements
Advertisements
प्रश्न
One diagonal of a rectangle is 18 cm. What is the length of its other diagonal?
उत्तर
∵ In a rectangle, diagonals are equal
⇒ AC = BD
Given, one diagonal of a rectangle = 18cm
∴ Other diagonal of a rectangle will be = 18cm
i.e. AC = BD = 18cm.
APPEARS IN
संबंधित प्रश्न
How many diagonals does following have?
A convex quadrilateral
In a quadrilateral, define of the following Adjacent angles .
Complete of the following, so as to make a true statement:
A quadrilateral has .... diagonals.
Complete of the following, so as to make a true statement:
A diagonal of a quadrilateral is a line segment that joins two ...... vertices of the quadrilateral.
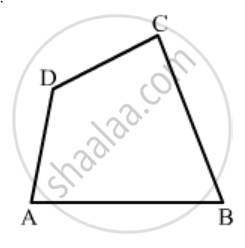
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of opposite angles.

In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite angles are there?
If the sum of the two angles of a quadrilateral is 180°. What is the sum of the remaining two angles?
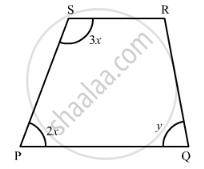
In the given figure, PQRS is an isosceles trapezium. Find x and y.
Complete the following statement by means of one of those given in brackets against each:
If both pairs of opposite sides of a quadrilateral are equal, then it is necessarily a ...............
If ABCD is a rectangle with ∠BAC = 32°, find the measure of ∠DBC.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
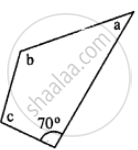
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
In a parallelogram ABCD, its diagonals AC and BD intersect each other at point O.
If AC = 12 cm and BD = 9 cm ; find; lengths of OA and OD.
ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
A quadrilateral can be drawn when all the four angles and one side is given.
In given figure, name any four angles that appear to be acute angles.
What conclusion can be drawn from part of given figure, if DB is the bisector of ∠ADC?
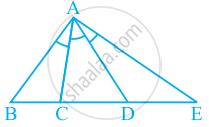
An angle is said to be trisected, if it is divided into three equal parts. If in the given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE?