Advertisements
Advertisements
प्रश्न
Plot a graph showing the variation of coulomb force (F) versus ,`(1/r^2)` where r is the distance between the two charges of each pair of charges: (1 μC, 2 μC) and (2 μC, − 3 μC). Interpret the graphs obtained.
उत्तर
I am answering it as Graph between F vs `1/r^2`for (1μC, 2μC)
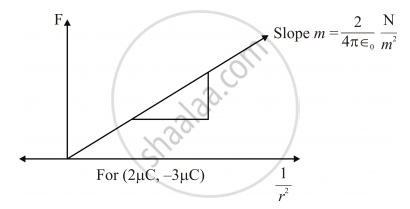
For (2μC − 3μC)
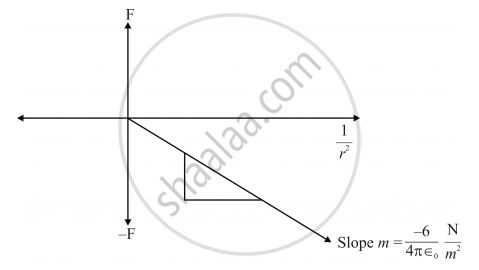
Interpretation
Graphs show that `F ∝ 1/r^2`
-
Slope gives a constant value and depends only on nature of charges and medium.
-
Ist graph is for repulsive force in Ist quadrant and IInd graph is for attractive force in IVth quadrant i.e., F > 0 and F < 0 respectively.
APPEARS IN
संबंधित प्रश्न
Suppose that the particle is an electron projected with velocity vx = 2.0 × 106 m s−1. If E between the plates separated by 0.5 cm is 9.1 × 102 N/C, where will the electron strike the upper plate? (|e| = 1.6 × 10−19 C, me = 9.1 × 10−31 kg)
Suppose an attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2. Write down the dimensional formulae and appropriate SI units of C and k.
Two charged particles with charge 2.0 × 10−8 C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
Solve numerical example.
Three equal charges of 10×10-8 C respectively, each located at the corners of a right triangle whose sides are 15 cm, 20 cm, and 25cm respectively. Find the force exerted on the charge located at the 90° angle.
Explain in detail Coulomb’s law and its various aspects.
Three charges +Q, q, +Q are placed respectively, at distance, 0, d/2 and d from the origin, on the X-axis. If the net force experienced by +Q, placed at x = 0, is zero then value of q is ____________.
For charges q1 and q2 separated by a distance R the magnitude of the electrostatic force is given by ______.
Two charges q and – 3q are placed fixed on x-axis separated by distance ‘d’. Where should a third charge 2q be placed such that it will not experience any force?
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
Two point charges +2 C and +6 C repel each other with a force of 12 N. If a charge of -4 C is given to each of these charges, then the force now is ______.
