Advertisements
Advertisements
प्रश्न
Solve numerical example.
Three equal charges of 10×10-8 C respectively, each located at the corners of a right triangle whose sides are 15 cm, 20 cm, and 25cm respectively. Find the force exerted on the charge located at the 90° angle.
उत्तर
Given: qA = qB = qC = 10 × 10-8 C
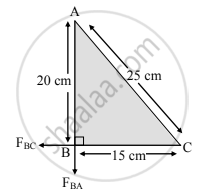
Force on B due to A,
`vec"F"_"BA"=1/(4πε_0)("q"_"A""q"_"B")/(("r"_"AB"^2))`
= `9 × 10^9xx((10xx10^-8)^2)/(20xx10^-2)^2`
= 2.25 × 10−3 N
Force on B due to C,
`vec"F"_"BC"=1/(4πε_0)("q"_"C""q"_"B")/(("r"_"BC"^2))`
= `9xx10^9xx((10xx10^-8)^2)/(15xx10^-2)^2`
= 4 × 10−3 N
∴ Resultant force on point B,
|FB| = `sqrt("F"_"BA"^2+"F"_"BC"^2+2"F"_"BA"."F"_"BC"cos 90)`
= `sqrt((2.25xx10^-3)^2+(4xx10^-3)^2)`
= 4.589 × 10−3 N
Force exerted on charge at point B is 4.589 × 10−3 N.
APPEARS IN
संबंधित प्रश्न
A particle of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in the fig.). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/(2m`"v"_"x"^2`).

Suppose that the particle is an electron projected with velocity vx = 2.0 × 106 m s−1. If E between the plates separated by 0.5 cm is 9.1 × 102 N/C, where will the electron strike the upper plate? (|e| = 1.6 × 10−19 C, me = 9.1 × 10−31 kg)
Three-point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q

(b) Find out the amount of the work done to separate the charges at infinite distance.
Find the dimensional formula of ε0.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical. Find the surface charge density on the plate.
Suppose the second charge in the previous problem is −1.0 × 10−6 C. Locate the position where a third charge will not experience a net force.
NaCl molecule is bound due to the electric force between the sodium and the chlorine ions when one electron of sodium is transferred to chlorine. Taking the separation between the ions to be 2.75 × 10−8 cm, find the force of attraction between them. State the assumptions (if any) that you have made.
Find the ratio of the electrical and gravitational forces between two protons.
Three equal charges, 2.0 × 10−6 C each, are held at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the other two.
A particle with a charge of 2.0 × 10−4 C is placed directly below and at a separation of 10 cm from the bob of a simple pendulum at rest. The mass of the bob is 100 g. What charge should the bob be given so that the string becomes loose?
A particle A with a charge of 2.0 × 10−6 C is held fixed on a horizontal table. A second charged particle of mass 80 g stays in equilibrium on the table at a distance of 10 cm from the first charge. The coefficient of friction between the table and this second particle is μ = 0.2. Find the range within which the charge of this second particle may lie.
Two particles A and B, each carrying a charge Q, are held fixed with a separation dbetween them. A particle C of mass m and charge q is kept at the middle point of the line AB. Under what conditions will the particle C execute simple harmonic motion if it is released after such a small displacement? Find the time period of the oscillations if these conditions are satisfied.
Repeat the previous problem if the particle C is displaced through a distance x along the line AB.
Three identical charges, each with a value of 1.0 × 10−8 C, are placed at the corners of an equilateral triangle of side 20 cm. Find the electric field and potential at the centre of the triangle.
Define a unit charge.
Answer the following question.
What is relative permittivity?
Write a short note on superposition principle.
Two-point charges of + 0.2 µµC and -0.2 µµC are separated by 1 o8 m. What is the value of the electric field at an axial point at a distance of 0.1 m from their mid-point?
Two point charges +3 µC and +8 µC repel each other with a force of 40 N. If a charge of -5 µC is added to each of them, then force between them will become ______.
The ratio of the forces between two small spheres with constant charge (a) in air (b) in a medium of dielectric constant K is ______.
Two identical thin rings, each of radius a meter, are coaxially placed at a distance R meter apart. If Q1 coulomb and Q2 coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge q coulomb from the centre of one ring to that of the other is ______.
SI unit of permittivity of free space is ______.
A charge Q is divided into two parts of q and Q – q. If the coulomb repulsion between them when they are separated is to be maximum, the ratio of Q/q should be ______.
A spring of spring constant 5 × 103 N/m is stretched initially by 5 cm from the unstretched position. Then the work required to stretch it further by another 5 cm is:
Coulomb's law is given by F = k q1q2 rn where n is
The capacity of an isolate conducting sphere of radius R is proportional to
Electric charge of any system is ______.
Two point charges Q each are placed at a distance d apart. A third point charge q is placed at a distance x from the mid-point on the perpendicular bisector. The value of x at which charge q will experience the maximum Coulomb's force is ______.
Four charges equal to −Q are placed at the four a corners of a square and charge q is at its centre. If the system is in equilibrium, the value of q is ______.
