Advertisements
Advertisements
प्रश्न
Refer to the graphs in figure. Match the following.
| Graph | Characteristic |
(a) 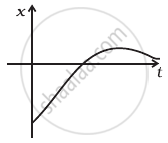 |
(i) has v > 0 and a < 0 throughout. |
(b) 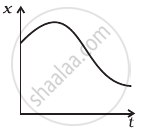 |
(ii) has x > 0 throughout and has a point with v = 0 and a point with a = 0. |
(c) 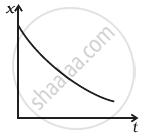 |
(iii) has a point with zero displacement for t > 0. |
(d) 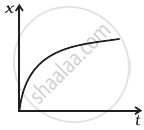 |
(iv) has v < 0 and a > 0. |
उत्तर
| Graph | Characteristic |
(a)  |
(iii) has a point with zero displacement for t > 0. |
(b)  |
(ii) has x > 0 throughout and has a point with v = 0 and a point with a = 0. |
(c)  |
(iv) has v < 0 and a > 0. |
(d)  |
(i) has v > 0 and a < 0 throughout. |
Explanation:
Let us pick graphs one by one.
In graph (a),
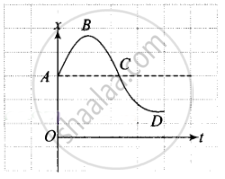
There is a point (B) on the curve for which displacement is zero. So curve, (a) matches with (iii).

In graph (b),
In this graph, x is positive (> 0) throughout and at point B the highest point of curve the slope of curve is zero. It means at this point v = dx/dt = 0 . Also at point C the dt
curvature changes, it means at this point the acceleration of the particle should be zero or a = 0, So curve (b) matches with (ii).
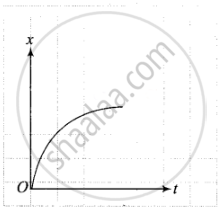
In graph (c),
In this graph the slope is always negative, hence velocity will be negative or v < 0. Also, x-t graph opens up, it represents positive acceleration. So curve (c) matches with (iv).

In graph (d),
In this graph the slope is always positive, hence velocity will be positive or v > 0. Also, x-t graph opens down, it representing negative acceleration. So curve (d) matches with (i).
APPEARS IN
संबंधित प्रश्न
Two projectiles A and B are projected with angle of projection 15° for the projectile A and 45° for the projectile B. If RA and RB be the horizontal range for the two projectiles, then
A particle moves along the X-axis as x = u (t − 2 s) + a (t − 2 s)2.
(a) the initial velocity of the particle is u
(b) the acceleration of the particle is a
(c) the acceleration of the particle is 2a
(d) at t = 2 s particle is at the origin.
A man has to go 50 m due north, 40 m due east and 20 m due south to reach a field. (a) What distance he has to walk to reach the field? (b) What is his displacement from his house to the field?
A particle starts from the origin, goes along the X-axis to the point (20 m, 0) and then return along the same line to the point (−20 m, 0). Find the distance and displacement of the particle during the trip.
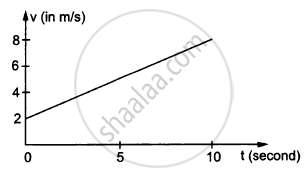
In the following figure Shows the graph of velocity versus time for a particle going along the X-axis. Find the acceleration
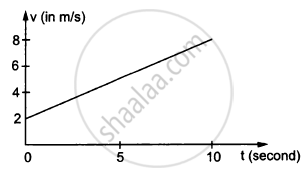
In the following figure Shows the graph of velocity versus time for a particle going along the X-axis. Find the displacement in 0 to 10 s.
A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the (horizontal) distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building? (take g = 10 m/s2)
The velocity-displacement graph of a particle is shown in figure.
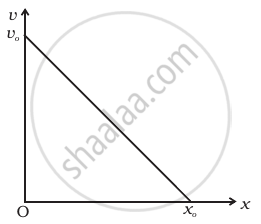
- Write the relation between v and x.
- Obtain the relation between acceleration and displacement and plot it.
Ship A is sailing towards the northeast with velocity `vecv = 30hati + 50hatj` km/hr where `hati` points east and `hatj`, north. Ship B is at a distance of 80 km east and 150 km north of Ship A and is sailing west at 10 km/hr. A will be at the minimum distance from B in ______.
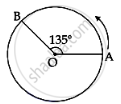
A person moved from A to B on a circular path as shown in figure. If the distance travelled by him is 60 m, then the magnitude of displacement would be: (Given cos135° = - 0.7)