Advertisements
Advertisements
प्रश्न
रेखाओं y = x, 3y = x और x + y = 8 से बनने वाले त्रिभुज के शीर्षों के निर्देशांक आलेखीय विधि से निर्धारित कीजिए।
उत्तर
दिए गए रैखिक समीकरण हैं।
y = x ......(i)
3y = x ......(ii)
और x + y = 8 ......(iii)
रेखा y = x के लिए तालिका,
| x | 0 | 1 | 2 |
| y | 0 | 1 | 2 |
रेखा x = 3y के लिए तालिका,
| x | 0 | 3 | 6 |
| y | 0 | 1 | 2 |
रेखा x + y = 8 के लिए तालिका
| x | 0 | 4 | 8 |
| y | 8 | 4 | 0 |
बिंदु A(1, 1), B(2, 2), C(3, 1), D(6, 2) को आलेखित करने पर, हमें सीधी रेखाएँ AB और CD प्राप्त होती हैं।
इसी प्रकार, बिंदु P(0, 8), Q(4, 4) और R(8, 0) को आलेखित करने पर, हमें सीधी रेखा PQR प्राप्त होती है।
AB और CD रेखा PR को क्रमश: Q और D पर प्रतिच्छेद करते हैं।
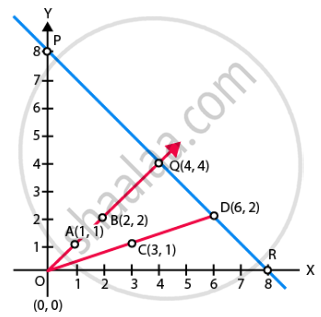
अत:, ∆OQD इन रेखाओं से बनता है।
इसलिए, दी गई रेखाओं से बने ∆OQD के शीर्ष O(0, 0), Q(4, 4) और D(6, 2) हैं।
APPEARS IN
संबंधित प्रश्न
निम्न समस्या में रैखिक समीकरण के युग्म बनाइए और उसके ग्राफीय विधि से हल ज्ञात कीजिए।
कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक हो, तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
निम्न रैखिक समीकरणों के युग्मों में से कौन से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
2x + y - 6 = 0, 4x - 2y - 4 = 0
समीकरणों x - y + 1 = 0 और 3x + 2y - 12 = 0 का ग्राफ खींचिए। x - अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।
समीकरणों 5x - y = 5 और 3x - y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
क्या समीकरणों के निम्नलिखित युग्म का कोई हल नहीं है? अपने उत्तर का औचित्य दीजिए।
x = 2y, y = 2x
क्या समीकरणों के निम्नलिखित युग्म का कोई हल नहीं है? अपने उत्तर का औचित्य दीजिए।
`3x + y - 3 = 0, 2x + 2/3y` = 2
क्या निम्नलिखित समीकरण संपाती रेखाओं का एक युग्म निरूपित करती है? अपने उत्तर का औचित्य दीजिए।
`3x + 1/7y = 3, 7x + 3y = 7`
क्या रैखिक समीकरणों के निम्नलिखित युग्म संगत हैं? अपने उत्तरों का औचित्य दीजिए।
–3x – 4y = 12, 4y + 3x = 12
λ के किस (किन) मान (मानों) के लिए रैखिक समीकरण-युग्म
λx + y = λ2
x + λy = 1
दो चरों वाले रैखिक समीकरणों के युग्म का कोई हल नहीं होगा?
λ के किस (किन) मान (मानों) के लिए रैखिक समीकरण-युग्म
λx + y = λ2
x + λy = 1
दो चरों वाले रैखिक समीकरणों के युग्म का एक अद्वितीय हल होगा?
