Advertisements
Advertisements
प्रश्न
समीकरण x = 3, x = 5 और 2x – y – 4 = 0 के आलेख खींचिए। इन रेखाओं और x-अक्ष द्वारा बनाए गए चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
उत्तर
रेखाओं x = 3, x = 5 और 2x – y – 4 = 0 का समीकरण दिया गया है।
रेखा 2x – y – 4 = 0 के लिए तालिका
| x | 0 | 2 |
| y | –4 | 0 |
ग्राफ आलेखित करने पर, हमें प्राप्त होता है,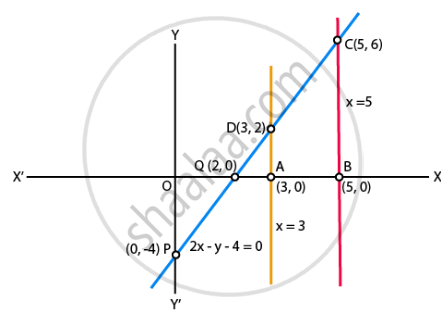
∴ चतुर्भुज ABCD का क्षेत्रफल = `1/2` × समानांतर रेखाओं के बीच की दूरी (AB) × (AD + BC) ...[चूँकि, चतुर्भुज ABCD एक समलंब है]
= `1/2 xx 2 xx (6 + 2)` ...[∵ AB = OB – OA = 5 – 3 = 2, AD = 2 and BC = 6]
= 8 वर्ग इकाई
APPEARS IN
संबंधित प्रश्न
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरण के युग्म संगत हैं या असंगत:
5x - 3y = 11; -10x + 6y = -22
निम्न रैखिक समीकरणों के युग्मों में से कौन से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
x + y = 5, 2x + 2y = 10
समीकरणों 5x - y = 5 और 3x - y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
क्या निम्नलिखित समीकरण संपाती रेखाओं का एक युग्म निरूपित करती है? अपने उत्तर का औचित्य दीजिए।
`3x + 1/7y = 3, 7x + 3y = 7`
क्या निम्नलिखित समीकरण संपाती रेखाओं का एक युग्म निरूपित करती है? अपने उत्तर का औचित्य दीजिए।
–2x – 3y = 1, 6y + 4x = – 2
क्या रैखिक समीकरणों के निम्नलिखित युग्म संगत हैं? अपने उत्तरों का औचित्य दीजिए।
समीकरण λx + 3y = –7, 2x + 6y = 14 के युग्म के अपरिमित रूप से अनेक हल होने के लिए, λ का मान 1 होना चाहिए। क्या यह कथन सत्य है? कारण दीजिए।
k के किस (किन) मान (मानों) के लिए, समीकरण-युग्म
kx + 3y = k – 3
12x + ky = k
का कोई हल नहीं होगा ?
रैखिक समीकरण x + y = 2 और 2x – y = 1 के युग्म के हल को निरूपित करने वाले बिंदु से होकर जाने वाली एक रेखा की समीकरण ज्ञात कीजिए। हम ऐसी कितनी रेखाएँ ज्ञात कर सकते हैं?
निम्नलिखित समीकरण-युग्म को आलेखीय रूप से हल कीजिए:
2x + y = 6, 2x – y + 2 = 0
उन दो त्रिभुजों के क्षेत्रफलों का अनुपात ज्ञात कीजिए, जो इन समीकरणों को निरूपित करने वाली रेखाओं द्वारा क्रमश: x-अक्ष और y-अक्ष द्वारा बनाए जाते हैं।
