Advertisements
Advertisements
प्रश्न
Select the correct option from the given alternatives:
If the focus of the parabola is (0, –3) its directrix is y = 3 then its equation is
विकल्प
x2 = – 12y
x2 = 12y
y2 = 12x
y2 = −12x
उत्तर
x2 = – 12y
Explanation;
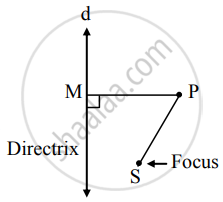
SP2 = PM2
∴ (x – 0)2 + (y + 3)2 = `|(y - 3)/sqrt(1)|^2`
∴ x2 + y2 + 6y + 9 = y2 – 6y + 9
∴ x2 = – 12y
APPEARS IN
संबंधित प्रश्न
Find co-ordinate of focus, equation of directrix, length of latus rectum and the co-ordinate of end points of latus rectum of the parabola:
y2 = –20x
Find co-ordinate of focus, equation of directrix, length of latus rectum and the co-ordinate of end points of latus rectum of the parabola:
x2 = –8y
Find the equation of the parabola with vertex at the origin, axis along X-axis and passing through the point (3, 4)
Find the equation of the parabola whose vertex is O(0, 0) and focus at (–7, 0).
Find the equation of the parabola with vertex at the origin, axis along X-axis and passing through the point (2, 3)
For the parabola 3y2 = 16x, find the parameter of the point (3, – 4).
For the parabola 3y2 = 16x, find the parameter of the point (27, –12).
Find coordinates of the point on the parabola. Also, find focal distance.
y2 = 12x whose parameter is `1/3`
Find coordinate of focus, vertex and equation of directrix and the axis of the parabola y = x2 – 2x + 3
Find the equation of tangent to the parabola y2 = 36x from the point (2, 9)
If the tangent drawn from the point (–6, 9) to the parabola y2 = kx are perpendicular to each other, find k
Find the equation of the locus of a point, the tangents from which to the parabola y2 = 18x are such that some of their slopes is –3
The tower of a bridge, hung in the form of a parabola have their tops 30 meters above the roadway and are 200 meters apart. If the cable is 5 meters above the roadway at the centre of the bridge, find the length of the vertical supporting cable 30 meters from the centre.
Select the correct option from the given alternatives:
The line y = mx + 1 is a tangent to the parabola y2 = 4x, if m is _______
Select the correct option from the given alternatives:
The length of latus rectum of the parabola x2 – 4x – 8y + 12 = 0 is _________
Select the correct option from the given alternatives:
Equation of the parabola with vertex at the origin and directrix x + 8 = 0 is __________
Answer the following:
For the following parabola, find focus, equation of the directrix, length of the latus rectum, and ends of the latus rectum:
5x2 = 24y
Answer the following:
Find the Cartesian coordinates of the point on the parabola y2 = 12x whose parameter is −3
Answer the following:
Find the co-ordinates of a point of the parabola y2 = 8x having focal distance 10
Answer the following:
Find the equations of the tangents to the parabola y2 = 9x through the point (4, 10).
Answer the following:
A line touches the circle x2 + y2 = 2 and the parabola y2 = 8x. Show that its equation is y = ± (x + 2).
Answer the following:
The slopes of the tangents drawn from P to the parabola y2 = 4ax are m1 and m2, show that `("m"_1 /"m"_2)` = k, where k is a constant.
Answer the following:
The tangent at point P on the parabola y2 = 4ax meets the y-axis in Q. If S is the focus, show that SP subtends a right angle at Q
Answer the following:
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) Distance between foci
(vi) distance between directrices of the curve
`x^2/144 - y^2/25` = 1
The length of latus-rectum of the parabola x2 + 2y = 8x - 7 is ______.
The area of the triangle formed by the lines joining vertex of the parabola x2 = 12y to the extremities of its latus rectum is ______.
Let P: y2 = 4ax, a > 0 be a parabola with focus S. Let the tangents to the parabola P make an angle of `π/4` with the line y = 3x + 5 touch the parabola P at A and B. Then the value of a for which A, B and S are collinear is ______.
If a line along a chord of the circle 4x2 + 4y2 + 120x + 675 = 0, passes through the point (–30, 0) and is tangent to the parabola y2 = 30x, then the length of this chord is ______.
If the normal at the point (1, 2) on the parabola y2 = 4x meets the parabola again at the point (t2, 2t), then t is equal to ______.
Which of the following are not parametric coordinates of any point on the parabola y2 = 4ax?
If the vertex = (2, 0) and the extremities of the latus rectum are (3, 2) and (3, –2) then the equation of the parabola is ______.
Through the vertex O of parabola y2 = 4x, chords OP and OQ are drawn at right angles to one another, where P and Q are points on the parabola. If the locus of middle point of PQ is y2 = 2(x – l), then value of l is ______.
Area of the equilateral triangle inscribed in the circle x2 + y2 – 7x + 9y + 5 = 0 is ______.
