Advertisements
Advertisements
प्रश्न
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्र फल और संपूर्ण पृष्ठीय क्षेत्र फल के उन सूत्रों को सिद्ध कीजिए,
उत्तर
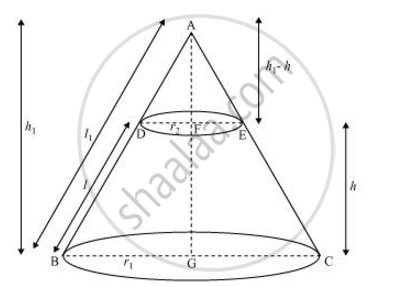
माना ABC एक शंकु है। एक छिन्नक DECB को उसके आधार के समांतर समतल द्वारा काटा जाता है। मान लीजिए r1 और r2 शंकु के छिन्नक के सिरों की त्रिज्याएँ हैं और h शंकु के छिन्नक की ऊँचाई हैं।
In ΔABG and ΔADF, DF||BG
∴ ΔABG ∼ ΔADF
DF/BG = AF/AG =AD/AB
`r_2/r_1 = (h_1-h)/h_1 =(l_1-l)/l_1`
`r_2/r_1 = 1- h/h_1 = 1 - 1/l_1`
`l - l/l_1= r_2/r_1`
`l/l_1 =1-r_2/r_1 =(r_1-r_2)/r_1`
`l_1/l = r_1/(r_1-r_2)`
`l_1 = (r_1l)/(r_1-r_2)`
छिन्नक का CSA DECB = शंकु ABC का CSA - CSA शंकु ADE
`= pir_1l_1 - pir_2(l_1-l)`
`=pir_1((lr_1)/(r_1-r_2))-pir_2[(r_1l)/(r_1-r_2)-l]`
`= (pir_1^2l)/(r_1-r_2) - pir_2((r_1l-r_1l+r_2l)/(r_1-r_2))`
`=(pir_1^2l)/(r_1-r_2)-(pir_2^2l)/(r_1-r_2)`
`= pil[(r_1^2-r_2^2)/(r_1-r_2)]`
छिन्नक का सीएसए = Π(r1 + r2)l
छिन्नक का कुल पृष्ठीय क्षेत्रफल = छिन्नक का CSA + ऊपरी वृत्ताकार सिरे का क्षेत्रफल + निचले वृत्ताकार सिरे का क्षेत्रफल
`= pi(r_1+r_2)l+pir_2^2+pir_1^2`
`=pi[(r_1+r_2)l+r_1^2+r_2^2]`
APPEARS IN
संबंधित प्रश्न
धातु की चादर से बना और ऊपर से खुला एक बर्तन शंकु के एक छिन्नक के आकार का है, जिसकी ऊँचाई 16 सेमी है तथा निचले और ऊपरी सिरों की त्रिज्याएँ क्रमश: 8 सेमी और 20 सेमी हैं। 20 रु प्रति लीटर की दर से, इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। साथ ही, इस बर्तन को बनाने के लिए प्रयुक्त धातु की चादर का मूल्य 8 रु प्रति 100 वर्ग सेमी की दर से ज्ञात कीजिए। [उपयोग π = 3.14]
एक गिलास का आकार प्रायः निम्न रूप का होता है-

एक शंकु को उसके आधार के समांतर एक तल की सहायता से काटा जाता है और फिर तल के एक ओर बने शंकु को हटा दिया जाता है। तल के दूसरी ओर बचा हुआ नया भाग कहलाता है एक ______।
क्रमशः आंतरिक और बाहरी व्यास 4 cm और 8 cm वाले एक धातु के गोलाकार खोल को पिघलाकर आधार व्यास 8 cm के एक शंकु के आकार में ढाला जाता है। इस शंकु की ऊँचाई ______ है।
एक बाल्टी के दोनों वृत्ताकार सिरों के व्यास 44 cm और 24 cm हैं तथा बाल्टी की ऊँचाई 35 cm है। इस बाल्टी की धारिता ______ है।
एक लंब वृत्तीय शंकु में, उसके आधार के समांतर खींचे गये तल द्वारा काटा गया अनुप्रस्थ-काट होता है एक ______।
शंकु के एक छिन्नक का आयतन `1/3 pih[r_1^2 + r_2^2 - r_1r_2]` होता है, जहाँ h छिन्नक की ऊर्घ्वाधर ऊँचाई है और r1, r2 सिरों की त्रिज्याएँ हैं।
शंकु के एक छिन्नक का वक्र पृष्ठीय क्षेत्रफल πl (r1 + r2) होता है, जहाँ `l = sqrt(h^2 + (r_1 + r _2)^2)` है, r1 और r2 छिन्नक के दोनों सिरों की त्रिज्याएँ हैं तथा h ऊर्ध्वाधर ऊँचाई है।
धातु की एक खुली बाल्टी इस आकार जैसी है कि उसी धातु की चादर से बने बेलनाकार (खोखला) आधार पर एक शंकु का छिन्नक रखा हुआ है। इसके लिए प्रयुक्त धातु की चादर का पृष्ठीय क्षेत्रफल बराबर है :
शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल
कोई बाल्टी एक शंकु के छिन्नक के आकार की है और इसमें 28.490 लीटर पानी आ सकता है। इसके ऊपरी और निचले सिरों की त्रिज्याएँ क्रमशः 28 cm और 21 cm हैं। इस बाल्टी की ऊँचाई ज्ञात कीजिए।
