Advertisements
Advertisements
प्रश्न
Show that A(–4, –7), B (–1, 2), C (8, 5) and D (5, –4) are the vertices of a parallelogram.
उत्तर
The given points are A(–4, –7), B(–1, 2), C(8, 5) and D(5, –4).
Slope of AB = \[\frac{2 - \left( - 7 \right)}{- 1 - \left( - 4 \right)} = \frac{9}{3} = 3\]
Slope of BC = \[\frac{5 - 2}{8 - \left( - 1 \right)} = \frac{3}{9} = \frac{1}{3}\]
Slope of CD = \[\frac{- 4 - 5}{5 - 8} = \frac{- 9}{- 3} = 3\]
Slope of AD = \[\frac{- 4 - \left( - 7 \right)}{5 - \left( - 4 \right)} = \frac{3}{9} = \frac{1}{3}\]
Slope of AB = Slope of CD
Slope of BC = Slope of AD
So, AB || CD and BC || AD
Hence, ABCD is a parallelogram.
APPEARS IN
संबंधित प्रश्न
Find the slope of the line passing through the points A(-2, 1) and B(0, 3).
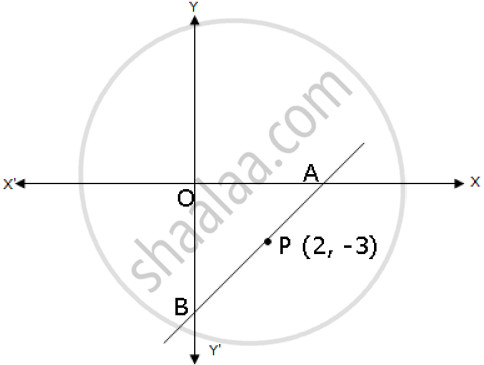
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
Find the slope of the line perpendicular to AB if : A = (0, −5) and B = (−2, 4)
Without using the distance formula, show that the points A(4, −2), B(−4, 4) and C(10, 6) are the vertices of a right-angled triangle.
(−2, 4), (4, 8), (10, 7) and (11, –5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
The points (−3, 2), (2, −1) and (a, 4) are collinear. Find a.
Find the slope and the inclination of the line AB if : A = `(-1, 2sqrt(3))` and B = `(-2, sqrt(3))`
Find the value of k for which the lines kx – 5y + 4 = 0 and 5x – 2y + 5 = 0 are perpendicular to each other.
Find the slope of the lines passing through the given point.
T (0, –3) , S (0, 4)
Determine whether the following point is collinear.
D(–2, –3), E(1, 0), F(2, 1)
Determine whether the following point is collinear.
A(–4, 4), \[K\left( - 2, \frac{5}{2} \right),\] N (4, –2)
Find the type of the quadrilateral if points A(–4, –2), B(–3, –7) C(3, –2) and D(2, 3) are joined serially.
Find the slope of a line parallel to the given line 3x-2y = 5
Find the slope of a line parallel to the given line 4x-2y = 3
Find the slope of a line parallel to the given line 5x + 2y = 11
Find the slope and the y-intercept of the following line 4y = 5x - 8
Find the slope of the line passing through the points A(6, -2) and B(–3, 4).
Find the slope of a line having inclination 60°.
Find the Slope of the line having inclination 45°.
Show that the points A(- 2, 5), B(2, – 3) and C(0, 1) are collinear.
