Advertisements
Advertisements
प्रश्न
Show that the four points A, B, C, D with position vectors \[\vec{a,} \vec{b,} \vec{c,} \vec{d}\] respectively such that \[3 \vec{a} - 2 \vec{b} + 5 \vec{c} - 6 \vec{d} = 0,\] are coplanar. Also, find the position vector of the point of intersection of the line segments AC and BD.
उत्तर
Let AC and BD intersects at a point P We have,
\[3 \vec{a} - 2 b^\rightharpoonup + 5 c^\rightharpoonup - 6 d^\rightharpoonup = \vec{0} . \]
\[ \Rightarrow 3 \vec{a} + 5 \vec{c} = 2 \vec{b} + 6 \vec{d} \]
Since sum of coefficients on both sides of the above equation is 8 .
so we divide the equation on both sides by 8 .
\[ \Rightarrow \frac{3 \vec{a} + 5 \vec{c}}{8} = \frac{2 \vec{b} + 6 \vec{d}}{8}\]
\[ \Rightarrow \frac{3 \vec{a} + 5 \vec{c}}{3 + 5} = \frac{2 \vec{b} + 6 \vec{d}}{2 + 6}\]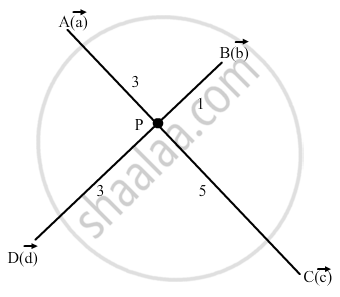
Therefore, P divides AC in the ratio of 3: 5 and P divides BD in the ratio of 2:6.
Therefore, position vector of the point of intersection of AC and BD will be \[\frac{3 \vec{a} + 5 \vec{c}}{8} = \frac{2 \vec{b} + 6 \vec{d}}{8}\]
APPEARS IN
संबंधित प्रश्न
The two vectors `hatj+hatk " and " 3hati-hatj+4hatk` represent the two sides AB and AC, respectively of a ∆ABC. Find the length of the median through A
Show that the four points P, Q, R, S with position vectors \[\vec{p}\], \[\vec{q}\], \[\vec{r}\], \[\vec{s}\] respectively such that 5 \[\vec{p}\] − 2 \[\vec{q}\] + 6 \[\vec{r}\] − 9 \[\vec{s}\] \[\vec{0}\], are coplanar. Also, find the position vector of the point of intersection of the line segments PR and QS.
The vertices A, B, C of triangle ABC have respectively position vectors \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] with respect to a given origin O. Show that the point D where the bisector of ∠ A meets BC has position vector \[\vec{d} = \frac{\beta \vec{b} + \gamma \vec{c}}{\beta + \gamma},\text{ where }\beta = \left| \vec{c} - \vec{a} \right| \text{ and, }\gamma = \left| \vec{a} - \vec{b} \right|\]
Hence, deduce that the incentre I has position vector
\[\frac{\alpha \vec{a} + \beta \vec{b} + \gamma \vec{c}}{\alpha + \beta + \gamma},\text{ where }\alpha = \left| \vec{b} - \vec{c} \right|\]
Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
Prove by vector method that the internal bisectors of the angles of a triangle are concurrent.
If the position vector of a point (−4, −3) be \[\vec{a,}\] find \[\left| \vec{a} \right|\]
Find the coordinates of the tip of the position vector which is equivalent to \[\vec{A} B\], where the coordinates of A and B are (−1, 3) and (−2, 1) respectively.
Find a unit vector in the direction of the resultant of the vectors
\[\hat{i} - \hat{j} + 3 \hat{k} , 2 \hat{i} + \hat{j} - 2 \hat{k} \text{ and }\hat{i} + 2 \hat{j} - 2 \hat{k} .\]
If \[\overrightarrow{PQ} = 3 \hat{i} + 2 \hat{j} - \hat{k}\] and the coordinates of P are (1, −1, 2), find the coordinates of Q.
If the vertices of a triangle are the points with position vectors \[a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k} , b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} , c_1 \hat{i} + c_2 \hat{j} + c_3 \hat{k} ,\]
what are the vectors determined by its sides? Find the length of these vectors.
Find the position vector of a point R which divides the line segment joining points \[P \left( \hat{i} + 2 \hat{j} + \hat{k} \right) \text{ and Q }\left( - \hat{i} + \hat{j} + \hat{k} \right)\] internally 2:1.
Find the position vector of a point R which divides the line segment joining points:
\[P \left( \hat{i} + 2 \hat{j} + \hat{k}\right) \text { and } Q \left( - \hat{i} + \hat{j} + \hat{k} \right)\] externally
Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q(4, 1, −2).
Show that the points A, B, C with position vectors \[\vec{a} - 2 \vec{b} + 3 \vec{c} , 2 \vec{a} + 3 \vec{b} - 4 \vec{c}\] and \[- 7 \vec{b} + 10 \vec{c}\] are collinear.
Prove that the points having position vectors \[\hat{i} + 2 \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k} , - 3 \hat{i} - 2 \hat{i} - 5 \hat{k}\] are collinear.
If the points with position vectors \[10 \hat{i} + 3 \hat{j} , 12 \hat{i} - 5 \hat{j}\text{ and a }\hat{i} + 11 \hat{j}\] are collinear, find the value of a.
If \[\vec{a,} \vec{b}\] are two non-collinear vectors prove that the points with position vectors \[\vec{a} + \vec{b,} \vec{a} - \vec{b}\text{ and }\vec{a} + \lambda \vec{b}\] are collinear for all real values of λ.
Show that the points whose position vectors are as given below are collinear:
\[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k} \text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\]
Show that the points whose position vectors are as given below are collinear: \[3 \hat{i} - 2 \hat{j} + 4 \hat{k}, \hat{i} + \hat{j} + \hat{k}\text{ and }- \hat{i} + 4 \hat{j} - 2 \hat{k}\]
Show that the four points having position vectors
\[6 \hat{i} - 7 \hat{j} , 16 \hat{i} - 19 \hat{j} - 4 \hat{k} , 3 \hat{j} - 6 \hat{k} , 2 \hat{i} - 5 \hat{j} + 10 \hat{k}\] are coplanar.
Show that the four points A, B, C and D with position vectors \[\vec{a}\], \[\vec{b}\], \[\vec{c}\], \[\vec{d}\] respectively are coplanar if and only if \[3 \vec{a} - 2 \vec{b} + \vec{c} - 2 \vec{d} = \vec{0} .\]
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are position vectors of the points A, B and C respectively, write the value of \[\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{AC} .\]
Find the position vector of the point which divides the join of points with position vectors `vec"a" + 3vec"b" and vec"a"- vec"b"` internally in the ratio 1 : 3.
X and Y are two points with position vectors `3vec("a") + vec("b")` and `vec("a")-3vec("b")`respectively. Write the position vector of a point Z which divides the line segment XY in the ratio 2 : 1 externally.
Find the value of x such that the four-point with position vectors,
`"A"(3hat"i"+2hat"j"+hat"k"),"B" (4hat"i"+"x"hat"j"+5hat"k"),"c" (4hat"i"+2hat"j"-2hat"k")`and`"D"(6hat"i"+5hat"j"-hat"k")`are coplaner.
Position vector of the mid-point of line segment AB is `3hati + 2hatj - 3hatk`. If position vector of the point A is `2hati + 3hatj - 4hatk`, then position vector of the point B is ______.
