Show that the Four Points A, B, C, D with Position Vectors → a , → B , → C , → D Respectively Such that - Mathematics

प्रश्न

Show that the four points A, B, C, D with position vectors $\vec{a,} \vec{b,} \vec{c,} \vec{d}$ respectively such that $3 \vec{a} - 2 \vec{b} + 5 \vec{c} - 6 \vec{d} = 0,$ are coplanar. Also, find the position vector of the point of intersection of the line segments AC and BD.

थोडक्यात उत्तर

उत्तर

Let AC and BD intersects at a point P We have,
$3 \vec{a} - 2 b^{⇀} + 5 c^{⇀} - 6 d^{⇀} = \vec{0} .$
$\Rightarrow 3 \vec{a} + 5 \vec{c} = 2 \vec{b} + 6 \vec{d}$
Since sum of coefficients on both sides of the above equation is 8 .
so we divide the equation on both sides by 8 .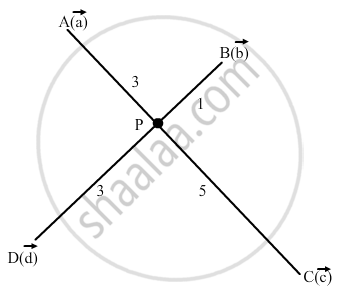
$\Rightarrow \frac{3 \vec{a} + 5 \vec{c}}{8} = \frac{2 \vec{b} + 6 \vec{d}}{8}$
$\Rightarrow \frac{3 \vec{a} + 5 \vec{c}}{3 + 5} = \frac{2 \vec{b} + 6 \vec{d}}{2 + 6}$

Therefore, P divides AC in the ratio of 3: 5 and P divides BD in the ratio of 2:6.
Therefore, position vector of the point of intersection of AC and BD will be $\frac{3 \vec{a} + 5 \vec{c}}{8} = \frac{2 \vec{b} + 6 \vec{d}}{8}$

shaalaa.com

Position Vector of a Point Dividing a Line Segment in a Given Ratio

या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?

Q 4 Q 3 Q 5

पाठ 23: Algebra of Vectors - Exercise 23.3 [पृष्ठ २४]

APPEARS IN

आरडी शर्मा Mathematics [English] Class 12

पाठ 23 Algebra of Vectors
Exercise 23.3 | Q 4 | पृष्ठ २४

संबंधित प्रश्‍न

The two vectors $\hat{j} + \hat{k} and 3 \hat{i} - \hat{j} + 4 \hat{k}$ represent the two sides AB and AC, respectively of a ∆ABC. Find the length of the median through A

Find the position vector of a point R which divides the line joining the two points P and Q with position vectors $\vec{O P} = 2 \vec{a} + \vec{b}$ and $\vec{O Q} = \vec{a} - 2 \vec{b}$ , respectively in the ratio 1 : 2 internally and externally.

If $\vec{a,} \vec{b}$ are the position vectors of A, B respectively, find the position vector of a point C in AB produced such that AC = 3 AB and that a point D in BA produced such that BD = 2BA.

Show that the four points P, Q, R, S with position vectors $\vec{p}$ , $\vec{q}$ , $\vec{r}$ , $\vec{s}$ respectively such that 5 $\vec{p}$ − 2 $\vec{q}$ + 6 $\vec{r}$ − 9 $\vec{s}$ $\vec{0}$ , are coplanar. Also, find the position vector of the point of intersection of the line segments PR and QS.

The vertices A, B, C of triangle ABC have respectively position vectors $\vec{a}$ , $\vec{b}$ , $\vec{c}$ with respect to a given origin O. Show that the point D where the bisector of ∠ A meets BC has position vector $\vec{d} = \frac{β \vec{b} + γ \vec{c}}{β + γ}, where β = | \vec{c} - \vec{a} | and, γ = | \vec{a} - \vec{b} |$
Hence, deduce that the incentre I has position vector
$\frac{α \vec{a} + β \vec{b} + γ \vec{c}}{α + β + γ}, where α = | \vec{b} - \vec{c} |$

Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.

Prove by vector method that the internal bisectors of the angles of a triangle are concurrent.

If the position vector of a point (−4, −3) be $\vec{a,}$ find $| \vec{a} |$

If the position vector $\vec{a}$ of a point (12, n) is such that $| \vec{a} |$ = 13, find the value (s) of n.

Find the coordinates of the tip of the position vector which is equivalent to $\vec{A} B$ , where the coordinates of A and B are (−1, 3) and (−2, 1) respectively.

If $\vec{a}$ be the position vector whose tip is (5, −3), find the coordinates of a point B such that $\vec{A B} =$ $\vec{a}$ , the coordinates of A being (4, −1).

Show that the points 2 $\hat{i}, - \hat{i} - 4$ $\hat{j}$ and $- \hat{i} + 4 \hat{j}$ form an isosceles triangle.

Find a unit vector in the direction of the resultant of the vectors
$\hat{i} - \hat{j} + 3 \hat{k}, 2 \hat{i} + \hat{j} - 2 \hat{k} and \hat{i} + 2 \hat{j} - 2 \hat{k} .$

If $\vec{P Q} = 3 \hat{i} + 2 \hat{j} - \hat{k}$ and the coordinates of P are (1, −1, 2), find the coordinates of Q.

Find the position vector of a point R which divides the line segment joining points $P (\hat{i} + 2 \hat{j} + \hat{k}) and Q (- \hat{i} + \hat{j} + \hat{k})$ internally 2:1.

Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q(4, 1, −2).

Show that the points A, B, C with position vectors $\vec{a} - 2 \vec{b} + 3 \vec{c}, 2 \vec{a} + 3 \vec{b} - 4 \vec{c}$ and $- 7 \vec{b} + 10 \vec{c}$ are collinear.

If the points A(m, −1), B(2, 1) and C(4, 5) are collinear, find the value of m.

Show that the points whose position vectors are as given below are collinear: $3 \hat{i} - 2 \hat{j} + 4 \hat{k}, \hat{i} + \hat{j} + \hat{k} and - \hat{i} + 4 \hat{j} - 2 \hat{k}$

Show that the four points having position vectors
$6 \hat{i} - 7 \hat{j}, 16 \hat{i} - 19 \hat{j} - 4 \hat{k}, 3 \hat{j} - 6 \hat{k}, 2 \hat{i} - 5 \hat{j} + 10 \hat{k}$ are coplanar.

Show that the four points A, B, C and D with position vectors $\vec{a}$ , $\vec{b}$ , $\vec{c}$ , $\vec{d}$ respectively are coplanar if and only if $3 \vec{a} - 2 \vec{b} + \vec{c} - 2 \vec{d} = \vec{0} .$

Define position vector of a point.

Find the image P' of the point P having position vector $\hat{i} + 3 \hat{j} + 4 \hat{k}$ in the plane $\vec{r} . (2 \hat{i} - \hat{j} + \hat{k}) + 3 = 0 .$ Hence find the length of PP'.

Find the position vector of the point which divides the join of points with position vectors $\vec{a} + 3 \vec{b} and \vec{a} - \vec{b}$ internally in the ratio 1 : 3.

X and Y are two points with position vectors $3 \vec{a} + \vec{b}$ and $\vec{a} - 3 \vec{b}$ respectively. Write the position vector of a point Z which divides the line segment XY in the ratio 2 : 1 externally.

Find the position vector of a point R which divides the line joining the two points P and Q with position vectors $\vec{OP} = 2 \vec{a} + \vec{b}$ and $\vec{OQ} = \vec{a} - 2 \vec{b}$ , respectively, in the ratio 1:2 internally

Find the position vector of a point R which divides the line joining the two points P and Q with position vectors $\vec{OP} = 2 \vec{a} + \vec{b}$ and $\vec{OQ} = \vec{a} - 2 \vec{b}$ , respectively, in the ratio 1:2 externally

The position vector of the point which divides the join of points with position vectors $\vec{a} + \vec{b}$ and 2 $\vec{a} - \vec{b}$ in the ratio 1:2 is ______.

The position vector of the point which divides the join of points $2 \vec{a} - 3 \vec{b}$ and $\vec{a} + \vec{b}$ in the ratio 3:1 is ______.

Show that the Four Points A, B, C, D with Position Vectors → a , → B , → C , → D Respectively Such that - Mathematics

Advertisements

Advertisements

प्रश्न

उत्तर

APPEARS IN

संबंधित प्रश्‍न

Select a course

Show that the Four Points A, B, C, D with Position Vectors → a , → B , → C , → D Respectively Such that - Mathematics

Advertisements

Advertisements

प्रश्न

उत्तरShow Solution

APPEARS IN

संबंधित प्रश्‍न

Select a course

उत्तर