Advertisements
Advertisements
प्रश्न
Show that the four points P, Q, R, S with position vectors \[\vec{p}\], \[\vec{q}\], \[\vec{r}\], \[\vec{s}\] respectively such that 5 \[\vec{p}\] − 2 \[\vec{q}\] + 6 \[\vec{r}\] − 9 \[\vec{s}\] \[\vec{0}\], are coplanar. Also, find the position vector of the point of intersection of the line segments PR and QS.
उत्तर
Let the point of intersection of the line segments PR and QS is A. Then \[5 \vec{p} - 2 \vec{q} + 6 \vec{r} - 9 \vec{s} = \vec{0} . \]
\[ \Rightarrow 5 \vec{p} + 6 \vec{r} = 2 \vec{q} + 9 \vec{s} \]
the sum of the coefficients on both the sides of the above equation is 11 .
So, we divide the given equation with 11 .
\[ \Rightarrow \frac{5 \vec{p} + 6 \vec{r}}{11} = \frac{2 \vec{q} + 9 \vec{s}}{11}\]
\[\frac{5 \vec{p} + 6 \vec{r}}{5 + 6} = \frac{2 \vec{q} + 9 \vec{s}}{2 + 9}\]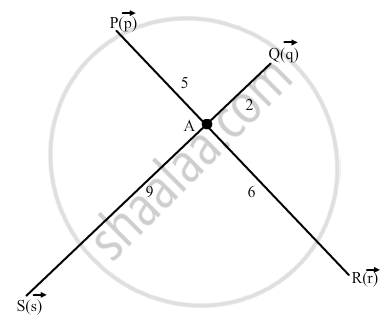
Therefore, A divides PR in the ratio of 5: 6 and QS in the ratio of \[2: 9\]
APPEARS IN
संबंधित प्रश्न
The two vectors `hatj+hatk " and " 3hati-hatj+4hatk` represent the two sides AB and AC, respectively of a ∆ABC. Find the length of the median through A
Find the position vector of a point R which divides the line joining the two points P and Q with position vectors \[\vec{OP} = 2 \vec{a} + \vec{b}\] and \[\vec{OQ} = \vec{a} - 2 \vec{b}\], respectively in the ratio 1 : 2 internally and externally.
If \[\vec{a,} \vec{b}\] are the position vectors of A, B respectively, find the position vector of a point C in AB produced such that AC = 3 AB and that a point D in BA produced such that BD = 2BA.
Show that the four points A, B, C, D with position vectors \[\vec{a,} \vec{b,} \vec{c,} \vec{d}\] respectively such that \[3 \vec{a} - 2 \vec{b} + 5 \vec{c} - 6 \vec{d} = 0,\] are coplanar. Also, find the position vector of the point of intersection of the line segments AC and BD.
Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
Prove by vector method that the internal bisectors of the angles of a triangle are concurrent.
If the position vector \[\vec{a}\] of a point (12, n) is such that \[\left| \vec{a} \right|\] = 13, find the value (s) of n.
Find the coordinates of the tip of the position vector which is equivalent to \[\vec{A} B\], where the coordinates of A and B are (−1, 3) and (−2, 1) respectively.
If the position vectors of the points A (3, 4), B (5, −6) and C (4, −1) are \[\vec{a,}\] \[\vec{b,}\] \[\vec{c}\] respectively, compute \[\vec{a} + 2 \vec{b} - 3 \vec{c}\].
Show that the points 2 \[\hat{i}, - \hat{i}-4 \] \[\hat{j}\] and \[-\hat{i}+4\hat{j}\] form an isosceles triangle.
Find a unit vector in the direction of the resultant of the vectors
\[\hat{i} - \hat{j} + 3 \hat{k} , 2 \hat{i} + \hat{j} - 2 \hat{k} \text{ and }\hat{i} + 2 \hat{j} - 2 \hat{k} .\]
If \[\overrightarrow{PQ} = 3 \hat{i} + 2 \hat{j} - \hat{k}\] and the coordinates of P are (1, −1, 2), find the coordinates of Q.
If the vertices of a triangle are the points with position vectors \[a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k} , b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} , c_1 \hat{i} + c_2 \hat{j} + c_3 \hat{k} ,\]
what are the vectors determined by its sides? Find the length of these vectors.
Find the position vector of a point R which divides the line segment joining points \[P \left( \hat{i} + 2 \hat{j} + \hat{k} \right) \text{ and Q }\left( - \hat{i} + \hat{j} + \hat{k} \right)\] internally 2:1.
Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q(4, 1, −2).
Prove that the points having position vectors \[\hat{i} + 2 \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k} , - 3 \hat{i} - 2 \hat{i} - 5 \hat{k}\] are collinear.
If the points with position vectors \[10 \hat{i} + 3 \hat{j} , 12 \hat{i} - 5 \hat{j}\text{ and a }\hat{i} + 11 \hat{j}\] are collinear, find the value of a.
If the points A(m, −1), B(2, 1) and C(4, 5) are collinear, find the value of m.
Show that the points whose position vectors are as given below are collinear:
\[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k} \text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\]
Show that the four points having position vectors
\[6 \hat{i} - 7 \hat{j} , 16 \hat{i} - 19 \hat{j} - 4 \hat{k} , 3 \hat{j} - 6 \hat{k} , 2 \hat{i} - 5 \hat{j} + 10 \hat{k}\] are coplanar.
Show that the four points A, B, C and D with position vectors \[\vec{a}\], \[\vec{b}\], \[\vec{c}\], \[\vec{d}\] respectively are coplanar if and only if \[3 \vec{a} - 2 \vec{b} + \vec{c} - 2 \vec{d} = \vec{0} .\]
If D is the mid-point of side BC of a triangle ABC such that \[\overrightarrow{AB} + \overrightarrow{AC} = \lambda \overrightarrow{AD} ,\] write the value of λ.
Find the position vector of the point which divides the join of points with position vectors `vec"a" + 3vec"b" and vec"a"- vec"b"` internally in the ratio 1 : 3.
X and Y are two points with position vectors `3vec("a") + vec("b")` and `vec("a")-3vec("b")`respectively. Write the position vector of a point Z which divides the line segment XY in the ratio 2 : 1 externally.
Find the value of x such that the four-point with position vectors,
`"A"(3hat"i"+2hat"j"+hat"k"),"B" (4hat"i"+"x"hat"j"+5hat"k"),"c" (4hat"i"+2hat"j"-2hat"k")`and`"D"(6hat"i"+5hat"j"-hat"k")`are coplaner.
Find the position vector of a point R which divides the line joining the two points P and Q with position vectors `vec"OP" = 2vec"a" + vec"b"` and `vec"OQ" = vec"a" - 2vec"b"`, respectively, in the ratio 1:2 internally
Find the position vector of a point R which divides the line joining the two points P and Q with position vectors `vec"OP" = 2vec"a" + vec"b"` and `vec"OQ" = vec"a" - 2vec"b"`, respectively, in the ratio 1:2 externally
The position vector of the point which divides the join of points with position vectors `vec"a" + vec"b"` and 2`vec"a" - vec"b"` in the ratio 1:2 is ______.
