Advertisements
Advertisements
प्रश्न
Show that the four points P, Q, R, S with position vectors \[\vec{p}\], \[\vec{q}\], \[\vec{r}\], \[\vec{s}\] respectively such that 5 \[\vec{p}\] − 2 \[\vec{q}\] + 6 \[\vec{r}\] − 9 \[\vec{s}\] \[\vec{0}\], are coplanar. Also, find the position vector of the point of intersection of the line segments PR and QS.
उत्तर
Let the point of intersection of the line segments PR and QS is A. Then \[5 \vec{p} - 2 \vec{q} + 6 \vec{r} - 9 \vec{s} = \vec{0} . \]
\[ \Rightarrow 5 \vec{p} + 6 \vec{r} = 2 \vec{q} + 9 \vec{s} \]
the sum of the coefficients on both the sides of the above equation is 11 .
So, we divide the given equation with 11 .
\[ \Rightarrow \frac{5 \vec{p} + 6 \vec{r}}{11} = \frac{2 \vec{q} + 9 \vec{s}}{11}\]
\[\frac{5 \vec{p} + 6 \vec{r}}{5 + 6} = \frac{2 \vec{q} + 9 \vec{s}}{2 + 9}\]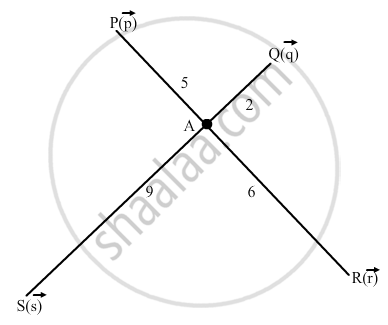
Therefore, A divides PR in the ratio of 5: 6 and QS in the ratio of \[2: 9\]
APPEARS IN
संबंधित प्रश्न
The two vectors `hatj+hatk " and " 3hati-hatj+4hatk` represent the two sides AB and AC, respectively of a ∆ABC. Find the length of the median through A
Show that the four points A, B, C, D with position vectors \[\vec{a,} \vec{b,} \vec{c,} \vec{d}\] respectively such that \[3 \vec{a} - 2 \vec{b} + 5 \vec{c} - 6 \vec{d} = 0,\] are coplanar. Also, find the position vector of the point of intersection of the line segments AC and BD.
The vertices A, B, C of triangle ABC have respectively position vectors \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] with respect to a given origin O. Show that the point D where the bisector of ∠ A meets BC has position vector \[\vec{d} = \frac{\beta \vec{b} + \gamma \vec{c}}{\beta + \gamma},\text{ where }\beta = \left| \vec{c} - \vec{a} \right| \text{ and, }\gamma = \left| \vec{a} - \vec{b} \right|\]
Hence, deduce that the incentre I has position vector
\[\frac{\alpha \vec{a} + \beta \vec{b} + \gamma \vec{c}}{\alpha + \beta + \gamma},\text{ where }\alpha = \left| \vec{b} - \vec{c} \right|\]
Prove by vector method that the internal bisectors of the angles of a triangle are concurrent.
If the position vector \[\vec{a}\] of a point (12, n) is such that \[\left| \vec{a} \right|\] = 13, find the value (s) of n.
Find the coordinates of the tip of the position vector which is equivalent to \[\vec{A} B\], where the coordinates of A and B are (−1, 3) and (−2, 1) respectively.
If the position vectors of the points A (3, 4), B (5, −6) and C (4, −1) are \[\vec{a,}\] \[\vec{b,}\] \[\vec{c}\] respectively, compute \[\vec{a} + 2 \vec{b} - 3 \vec{c}\].
If \[\vec{a}\] be the position vector whose tip is (5, −3), find the coordinates of a point B such that \[\overrightarrow{AB} =\] \[\vec{a}\], the coordinates of A being (4, −1).
Show that the points 2 \[\hat{i}, - \hat{i}-4 \] \[\hat{j}\] and \[-\hat{i}+4\hat{j}\] form an isosceles triangle.
The position vectors of points A, B and C are \[\lambda \hat{i} +\] 3 \[\hat{j}\],12\[\hat{i} + \mu\] \[\hat{j}\] and 11\[\hat{i} -\] 3 \[\hat{j}\] respectively. If C divides the line segment joining A and B in the ratio 3:1, find the values of \[\lambda\] and \[\mu\]
If \[\overrightarrow{PQ} = 3 \hat{i} + 2 \hat{j} - \hat{k}\] and the coordinates of P are (1, −1, 2), find the coordinates of Q.
Find the position vector of a point R which divides the line segment joining points \[P \left( \hat{i} + 2 \hat{j} + \hat{k} \right) \text{ and Q }\left( - \hat{i} + \hat{j} + \hat{k} \right)\] internally 2:1.
Find the position vector of a point R which divides the line segment joining points:
\[P \left( \hat{i} + 2 \hat{j} + \hat{k}\right) \text { and } Q \left( - \hat{i} + \hat{j} + \hat{k} \right)\] externally
Show that the points A, B, C with position vectors \[\vec{a} - 2 \vec{b} + 3 \vec{c} , 2 \vec{a} + 3 \vec{b} - 4 \vec{c}\] and \[- 7 \vec{b} + 10 \vec{c}\] are collinear.
If the points with position vectors \[10 \hat{i} + 3 \hat{j} , 12 \hat{i} - 5 \hat{j}\text{ and a }\hat{i} + 11 \hat{j}\] are collinear, find the value of a.
If \[\vec{a,} \vec{b}\] are two non-collinear vectors prove that the points with position vectors \[\vec{a} + \vec{b,} \vec{a} - \vec{b}\text{ and }\vec{a} + \lambda \vec{b}\] are collinear for all real values of λ.
Show that the points whose position vectors are as given below are collinear: \[3 \hat{i} - 2 \hat{j} + 4 \hat{k}, \hat{i} + \hat{j} + \hat{k}\text{ and }- \hat{i} + 4 \hat{j} - 2 \hat{k}\]
Show that the four points A, B, C and D with position vectors \[\vec{a}\], \[\vec{b}\], \[\vec{c}\], \[\vec{d}\] respectively are coplanar if and only if \[3 \vec{a} - 2 \vec{b} + \vec{c} - 2 \vec{d} = \vec{0} .\]
Define position vector of a point.
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are position vectors of the points A, B and C respectively, write the value of \[\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{AC} .\]
If D is the mid-point of side BC of a triangle ABC such that \[\overrightarrow{AB} + \overrightarrow{AC} = \lambda \overrightarrow{AD} ,\] write the value of λ.
Find the image P' of the point P having position vector `hati+ 3hatj+ 4hatk` in the plane `vecr. (2hati - hatj + hatk) + 3 = 0 .` Hence find the length of PP'.
Find the position vector of the point which divides the join of points with position vectors `vec"a" + 3vec"b" and vec"a"- vec"b"` internally in the ratio 1 : 3.
X and Y are two points with position vectors `3vec("a") + vec("b")` and `vec("a")-3vec("b")`respectively. Write the position vector of a point Z which divides the line segment XY in the ratio 2 : 1 externally.
Find the position vector of a point R which divides the line joining the two points P and Q with position vectors `vec"OP" = 2vec"a" + vec"b"` and `vec"OQ" = vec"a" - 2vec"b"`, respectively, in the ratio 1:2 internally
Find the position vector of a point R which divides the line joining the two points P and Q with position vectors `vec"OP" = 2vec"a" + vec"b"` and `vec"OQ" = vec"a" - 2vec"b"`, respectively, in the ratio 1:2 externally
The position vector of the point which divides the join of points with position vectors `vec"a" + vec"b"` and 2`vec"a" - vec"b"` in the ratio 1:2 is ______.
The position vector of the point which divides the join of points `2vec"a" - 3vec"b"` and `vec"a" + vec"b"` in the ratio 3:1 is ______.
Position vector of the mid-point of line segment AB is `3hati + 2hatj - 3hatk`. If position vector of the point A is `2hati + 3hatj - 4hatk`, then position vector of the point B is ______.
