Advertisements
Advertisements
प्रश्न
Show that the function f(x) = `{(x^2, x<=1),(1/2, x>1):}` is continuous at x = 1 but not differentiable.
उत्तर
Continuity at x = 1
`(x = 1)= x^2 = (1)^2 = 1`
`lim_(x->1^+) f(x) = lim_(x->1^+) 1/x = 1`
`lim_(x->1^-) f(x) = lim_(x->1^-) x^2 = 1`
`:. f(x = 1) = lim_(x->1^-) f(x) = lim_(x->1^+) f(x) = 1`
:. f(x) is continuous at x = 1
Now differentiable at x = 1
(R.H.D at x = 1) = `lim_(x->1^+) (f(x) - f(1))/(x -1)`
`=lim_(x->1) (1/x- 1)/(x - 1)`
`= lim_(x-> 1) (-(x-1) 1/x)/(x-1)`
`= = -1/1 = -1`
(L.H.D at x = 1) = `lim_(x -> 1^(-)) (f(x)-f(1))/(x-1)`
`= lim_(x->1^1) (x^2 -1)/(x - 1) = 2`
`:. l.H.D != R.H.D`
:. f(x) is not differentiable at x = 1
APPEARS IN
संबंधित प्रश्न
Discuss the continuity of the following functions. If the function have a removable discontinuity, redefine the function so as to remove the discontinuity
`f(x)=(4^x-e^x)/(6^x-1)` for x ≠ 0
`=log(2/3) ` for x=0
Find the values of p and q for which
f(x) = `{((1-sin^3x)/(3cos^2x),`
is continuous at x = π/2.
Examine the continuity of the function f(x) = 2x2 – 1 at x = 3.
Is the function f defined by f(x)= `{(x, if x<=1),(5, if x > 1):}` continuous at x = 0? At x = 1? At x = 2?
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|+3, if x<= -3),(-2x, if -3 < x < 3),(6x + 2, if x >= 3):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|/x , if x != 0),(0, if x = 0):}`
Find all points of discontinuity of f, where f is defined by `f (x) = {(x^10 - 1, if x<=1),(x^2, if x > 1):}`
Is the function defined by `f(x) = {(x+5, if x <= 1),(x -5, if x > 1):}` a continuous function?
Show that the function defined by g(x) = x = [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.
Determine if f defined by `f(x) = {(x^2 sin 1/x, "," if x != 0),(0, "," if x = 0):}` is a continuous function?
Examine the continuity of f, where f is defined by `f(x) = {(sin x - cos x, if x != 0),(-1, "," if x = 0):}`
In the following, determine the value of constant involved in the definition so that the given function is continuou:
The function f (x) = tan x is discontinuous on the set
Prove that `1/2 "cos"^(-1) ((1-"x")/(1+"x")) = "tan"^-1 sqrt"x"`
The number of discontinuous functions y(x) on [-2, 2] satisfying x2 + y2 = 4 is ____________.
Let f (x) `= (1 - "tan x")/(4"x" - pi), "x" ne pi/4, "x" in (0, pi/2).` If f(x) is continuous in `(0, pi/2), "then f"(pi/4) =` ____________.
If f(x) `= sqrt(4 + "x" - 2)/"x", "x" ne 0` be continuous at x = 0, then f(0) = ____________.
`lim_("x"-> 0) sqrt(1/2 (1 - "cos" 2"x"))/"x"` is equal to
The domain of the function f(x) = `""^(24 - x)C_(3x - 1) + ""^(40 - 6x)C_(8x - 10)` is
How many point of discontinuity for the following function for x ∈ R
`f(x) = {{:(x + 1",", if x ≥ 1),(x^2 + 1",", if x < 1):}`
`f(x) = {{:(x^10 - 1",", if x ≤ 1),(x^2",", if x > 1):}` is discontinuous at
Sin |x| is a continuous function for
If functions g and h are defined as
g(x) = `{{:(x^2 + 1, x∈Q),(px^2, x\cancel(∈)Q):}`
and h(x) = `{{:(px, x∈Q),(2x + q, x\cancel(∈)Q):}`
If (g + h)(x) is continuous at x = 1 and x = 3, then 3p + q is ______.
If f(x) = `{{:(cos ((π(sqrt(1 + x) - 1))/x)/x,",", x ≠ 0),(π/k,",", x = 0):}`
is continuous at x = 0, then k2 is equal to ______.
If the function f defined as f(x) = `1/x - (k - 1)/(e^(2x) - 1)` x ≠ 0, is continuous at x = 0, then the ordered pair (k, f(0)) is equal to ______.
The graph of the function f is shown below.
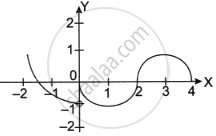
Of the following options, at what values of x is the function f NOT differentiable?
Consider the graph `y = x^(1/3)`
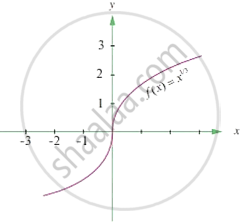
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
