Advertisements
Advertisements
प्रश्न
सीमा और नेहा ने एक ही स्थान से पूर्व और उत्तर दिशा में एक ही गति से चलना प्रारंभ किया, दो घंटे पश्चात उनके बीच की दूरी `15sqrt2` किमी हो तो उनकी प्रतिघंटा गति ज्ञात कीजिए।
उत्तर
आकृति में, मानो कि सीमा और नेहा ने बिंदु A से चलना प्रारंभ किया, रेख AB यह सीमा के द्वारा और रेख AC यह नेहा के द्वारा तय किया गया रास्ता है |
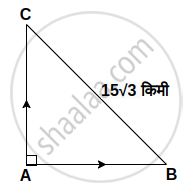
दो घंटे पश्चात्, सीमा बिंदु B पर पहुँचती है और नेहा बिंदु C पर पहुँचती है |
BC = `15sqrt2` किमी
सीमा और नेहा एक ही गति से चलना प्रारंभ करती है |
माना उन दोनों की गति x किमी/घंटा है |
∵ दूरी = चाल × समय
∴ दूरी AB = x × 2
∴ AB = 2x किमी
इसी प्रकार दूरी AC = x × 2
∴ AC = 2x किमी
समकोण ΔACB मे,
∴ पायथागोरस के प्रमेय से,
BC2 = AC2 + AB2
∴ `(15sqrt2)^2 = (2x)^2 + (2x)^2`
∴ `225 xx 2 = 4x^2 + 4x^2`
∴ `8x^2 = 225 xx 2`
∴ `x^2 = (225 xx 2)/8`
∴ `x^2 = 225/4`
∴ x = `15/2` ..............(दोनों पक्षों का वर्गमूल लेने पर)
∴ x = 7.5
∴ उनकी प्रतिघंटा चाल 7.5 किमी/घंटा है |
APPEARS IN
संबंधित प्रश्न
किसी वर्ग के विकर्ण की लंबाई 10 सेमी हो तो उसकी भुजा की लंबाई तथा परिमिति ज्ञात कीजिए।
किसी आयत की लंबाई 35 सेमी तथा चौड़ाई 12 सेमी हो तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
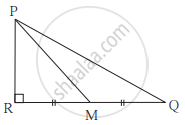
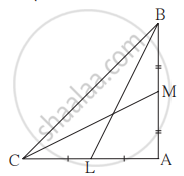
आकृति में M यह भुजा QR का मध्यबिंदु है। ∠PRQ = 90° तो सिद्ध कीजिए कि, PQ2 = 4PM2 - 3PR2
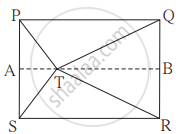
आकृति में दर्शाएनुसार बिंदु T यह आयत PQRS के अंतर्भाग में स्थित है। तो सिद्ध कीजिए कि, TS2 + TQ2 = TP2 + TR2 (आकृति में दर्शाएअनुसार रेख AB || भुजा SR ऐसा खींचिए कि A-T-B)
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
a, b, c भुजावाले त्रिभुज में यदि a2 + b2 = c2 हो तो वह त्रिभुज किस प्रकार का होगा?
किसी आयत की भुजाएँ क्रमश: 11 सेमी तथा 60 सेमी हों तो उसके विकर्ण की लंबाई ज्ञात कीजिए।
किसी आयत का क्षेत्रफल 192 वर्ग सेमी तथा उसकी लंबाई 16 सेमी हो, तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
किसी समबाहु त्रिभुज की ऊँचाई `sqrt3` सेमी हो, तो उस त्रिभुज के भुजा की लंबाई तथा उसकी परिमिति ज्ञात कीजिए।
ΔABC में ∠BAC = 90°, रेख BL तथा रेख CM, यह ΔABC की माध्यिकाएँ हों तो सिद्ध कीजिए कि, 4(BL2 + CM2) = 5 BC2
ΔABC में रेख AD ⊥ रेख BC और DB = 3CD, तो सिद्ध कीजिए कि : 2AB2 = 2AC2 + BC2