Advertisements
Advertisements
Question
सीमा और नेहा ने एक ही स्थान से पूर्व और उत्तर दिशा में एक ही गति से चलना प्रारंभ किया, दो घंटे पश्चात उनके बीच की दूरी `15sqrt2` किमी हो तो उनकी प्रतिघंटा गति ज्ञात कीजिए।
Solution
आकृति में, मानो कि सीमा और नेहा ने बिंदु A से चलना प्रारंभ किया, रेख AB यह सीमा के द्वारा और रेख AC यह नेहा के द्वारा तय किया गया रास्ता है |
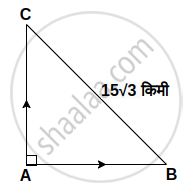
दो घंटे पश्चात्, सीमा बिंदु B पर पहुँचती है और नेहा बिंदु C पर पहुँचती है |
BC = `15sqrt2` किमी
सीमा और नेहा एक ही गति से चलना प्रारंभ करती है |
माना उन दोनों की गति x किमी/घंटा है |
∵ दूरी = चाल × समय
∴ दूरी AB = x × 2
∴ AB = 2x किमी
इसी प्रकार दूरी AC = x × 2
∴ AC = 2x किमी
समकोण ΔACB मे,
∴ पायथागोरस के प्रमेय से,
BC2 = AC2 + AB2
∴ `(15sqrt2)^2 = (2x)^2 + (2x)^2`
∴ `225 xx 2 = 4x^2 + 4x^2`
∴ `8x^2 = 225 xx 2`
∴ `x^2 = (225 xx 2)/8`
∴ `x^2 = 225/4`
∴ x = `15/2` ..............(दोनों पक्षों का वर्गमूल लेने पर)
∴ x = 7.5
∴ उनकी प्रतिघंटा चाल 7.5 किमी/घंटा है |
APPEARS IN
RELATED QUESTIONS
किसी वर्ग के विकर्ण की लंबाई 10 सेमी हो तो उसकी भुजा की लंबाई तथा परिमिति ज्ञात कीजिए।
आकृति में ∠DFE = 90°, रेख FG ⊥ रेख ED. यदि GD = 8, FG = 12, तो (1) EG (2) FD (3) EF का मान ज्ञात कीजिए।

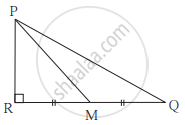
आकृति में M यह भुजा QR का मध्यबिंदु है। ∠PRQ = 90° तो सिद्ध कीजिए कि, PQ2 = 4PM2 - 3PR2
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
समकोण त्रिभुज में समकोण बनानेवाली भुजाओं के वर्गों का योगफल 169 हो तो उसके कर्ण की लंबाई कितनी होगी?
किसी आयत की भुजाएँ क्रमश: 11 सेमी तथा 60 सेमी हों तो उसके विकर्ण की लंबाई ज्ञात कीजिए।
किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाएँ क्रमश: 9 सेमी तथा 12 सेमी हों तो उस त्रिभुज के कर्ण की लंबाई ज्ञात कीजिए।
किसी आयत का क्षेत्रफल 192 वर्ग सेमी तथा उसकी लंबाई 16 सेमी हो, तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
किसी समबाहु त्रिभुज की ऊँचाई `sqrt3` सेमी हो, तो उस त्रिभुज के भुजा की लंबाई तथा उसकी परिमिति ज्ञात कीजिए।
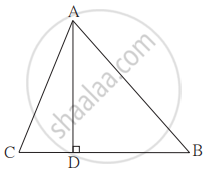
ΔABC में रेख AD ⊥ रेख BC और DB = 3CD, तो सिद्ध कीजिए कि : 2AB2 = 2AC2 + BC2
किसी समद्विबाहु त्रिभुज में सर्वांगसम भुजाओं की लंबाई 13 सेमी तथा आधार की लंबाई 10 सेमी हो तो उस त्रिभुज की माध्यिकाओं के संगमन बिंदु से आधार के सम्मुख शीर्षबिंदु तक की दूरी ज्ञात कीजिए।
