Advertisements
Advertisements
प्रश्न
Simplify the following:
x2 − 3x + 5 − \[\frac{1}{2}\] (3x2 − 5x + 7)
उत्तर
\[ x^2 - 3x + 5 - \frac{1}{2}\left( 3 x^2 - 5x + 7 \right)\]
\[ = x^2 - 3x + 5 - \frac{3 x^2}{2} + \frac{5x}{2} - \frac{7}{2}\]
\[ = x^2 - \frac{3 x^2}{2} - 3x + \frac{5x}{2} + 5 - \frac{7}{2} (\text { Collecting like terms })\]
\[ = \left( \frac{1 - 3}{2} \right) x^2 + \left( \frac{- 3 + 5}{2} \right)x + \left( \frac{10 - 7}{2} \right)\]
\[ = - \frac{x^2}{2} - \frac{x}{2} + \frac{3}{2}\]
Thus, the answer is \[- \frac{x^2}{2} - \frac{x}{2} + \frac{3}{2}\].
APPEARS IN
संबंधित प्रश्न
State whether a given pair of term is of like or unlike term.
1,100
State whether a given pair of term is of like or unlike term.
14xy, 42yx
State whether a given pair of term is of like or unlike term.
4m2p, 4mp2
Simplify the following:
[5 − 3x + 2y − (2x − y)] − (3x − 7y + 9)
Choose the pair of like terms
Which of the following is a binomial?
Which of the following are like terms?
Which of the following is a pair of like terms?
The unlike terms in perimeters of following figures are ______ and ______.
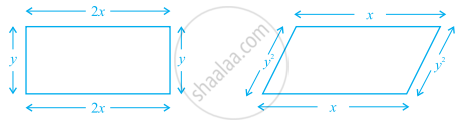
In like terms, variables and their powers are the same.
