Advertisements
Advertisements
प्रश्न
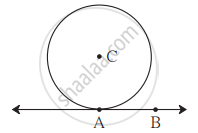
संलग्न आकृति में, C केंद्रवाले वृत्त की त्रिज्या 6 सेमी है। रेखा AB वृत्त को बिंदु A पर स्पर्श करता है। इस जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
(1) ∠CAB का माप कितने अंश है? क्यों?
(2) बिंदु C, रेखा AB से कितनी दूरी पर है? क्यों?
(3) यदि d(A, B) = 6 सेमी, तो d(B,C) ज्ञात कीजिए।
(4) ∠ABC का माप कितने अंश है? क्यों?
उत्तर
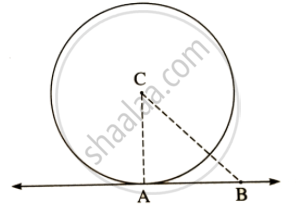
(1) रेख CA खींचो |
∠CAB = 90° .................(स्पर्श रेखा प्रमेय) ..........(1)
(2) रेख CA ⊥ रेखा AB ...........[(1) से]
CA = 6 सेमी .........(दिया है)
∴ रेखा AB से बिंदु C की दुरी 6 सेमी है |
(3) ΔCAB में,
∠CAB = 90° ...........[(1) से]
पायथागोरस के प्रमेय से,
CB2 = CA2 + AB2
∴ BC2 = 62 + 62
∴ BC2 = 36 + 36
∴ BC2 = 72
∴ BC = `6sqrt2` सेमी ................(दोनों पक्षों का वर्गमूल लेने पर)
d(B, C) = BC = `underline(6sqrt2)` सेमी |
(4) ΔABC में,
CA = AB .........(प्रत्येक का माप 6 सेमी है)
∠ABC = ∠ACB .........(समद्विबाहु त्रिभुज का प्रमेय)
मान लो, ∠ABC = ∠ACB = x
ΔABC में,
∠CAB + ∠ABC + ∠ACB = 180° .............(त्रिभुज के सभी कोणों के मापों का योग)
∴ 90° + x + x = 180°
∴ 2x° = 180° - 90°
∴ 2x° = 90°
∴ x = `90/2`
∴ x = 45°
∴ ∠ABC = 45°
APPEARS IN
संबंधित प्रश्न
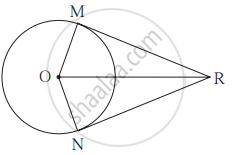
संलग्न आकृति में, O केंद्रवाले वृत्त के बाह्य भाग में स्थित बिंदु R से खींचे गए RM और RN स्पर्श रेखाखंड वृत्त को बिंदु M और N पर स्पर्श करते हैं। यदि l(O,R)= 10 सेमी तथा वृत्त की त्रिज्या 5 सेमी हो तो -
(1) प्रत्येक स्पर्श रेखाखंड की लंबाई कितनी होगी?
(2) ∠MRO का माप कितना होगा?
(3) ∠MRN का माप कितना होगा?
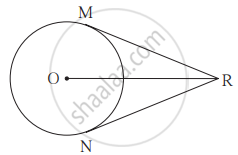
रेख RM और रेख RN, O केंद्रवाले वृत्त के स्पर्श रेखाखंड हैं। सिद्ध कीजिए की रेख OR, ∠MRN और ∠MON दोनों कोणों का समद्विभाजक है।
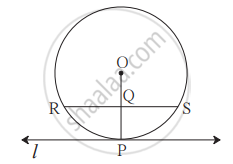
संलग्न आकृति में रेखा l, बिंदु O केंद्र वाले वृत्त को बिंदु P पर स्पर्श करती है। बिंदु Q त्रिज्या OP का मध्य बिंदु है। बिंदु Q से होकर जानेवाली जीवा RS || रेखा l। यदि RS = 12 सेमी हो, तो वृत्त की त्रिज्या ज्ञात कीजिए |