Advertisements
Advertisements
प्रश्न
Solve the following pair of linear equations
ax + by = c
bx + ay = 1 + c
उत्तर
ax + by = c … (1)
bx + ay = 1 + c … (2)
Multiplying equation (1) by a and equation (2) by b, we obtain
a2x + aby = ac … (3)
b2x + aby = b + bc … (4)
Subtracting equation (4) from equation (3),
(a2 − b2) x = ac − bc − b
`x = (c(a-b)-b)/(a^2 - b^2)`
From equation (1), we obtain
ax + by = c
`a{((c(a-b)-b))/(a^2-b^2)}+by = c`
`(ac(a-b)-ab)/(a^2-b^2)+by=c`
`by = c - (ac(a-b)-ab)/(a^2-b^2)`
`by = (a^2c-b^2c-a^2c+abc+ab)/(a^2-b^2)`
`by= (abc-b^2c+ab)/(a^2-b^2)`
`by = (bc(a-b)+ab)/(a^2-b^2)`
`y= (c(a-b)+a)/(a^2-b^2)`
APPEARS IN
संबंधित प्रश्न
Solve `\frac { 2 }{ x } + \frac { 1 }{ 3y } = \frac { 1}{ 5 }; \frac { 3 }{ x } + \frac { 2 }{ 3y } = 2` and also find ‘a’ for which y = ax – 2
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solve the following pair of linear equations: px + qy = p − q, qx − py = p + q
Solve the following pair of linear equations.
`x/a-y/b = 0`
ax + by = a2 + b2
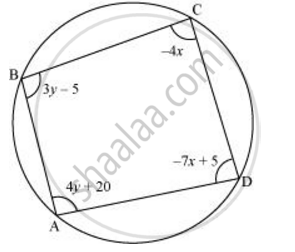
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
Find the value of following determinant.
`|(5,3), (-7,0)|`
A two-digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
The sum of a numerator and denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to 1/3. Find the fraction.
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
