Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
x + 2y + 1 = 0,
2x – 3y – 12 = 0.
उत्तर
The given equations are:
x + 2y + 1 = 0 …….(i)
2x – 3y – 12 = 0 …….(ii)
Here a1 = `1, b_1 = 2, c_1 = 1, a_2 = 2, b_2 = -3 and c_2 = -12`
By cross multiplication, we have:

∴ `x/([2 xx(-12)-1xx(-3)]) = y/([1xx2-1xx(-12)]) = 1/([1xx(-3)-2xx2])`
⇒`x/((-24+3))= y/((2+12)) = 1/((-3-4))`
⇒`x/((-21)) = y/((14)) = 1/((-7))`
⇒` x = (-21)/(-7)= 3, y = 14/(-7) = -2`
Hence, x = 3 and y = -2 is the required solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by cross-multiplication method.
ax + by = a – b; bx – ay = a + b
Solve the following system of equations by cross-multiplication method ax + by = 1; `bx + ay = \frac{(a+b)^{2}}{a^{2}+b^{2}-1`
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solve the following systems of equations:
`4/x + 3y = 14`
`3/x - 4y = 23`
Solve each of the following systems of equations by the method of cross-multiplication :
6(ax + by) = 3a + 2b
6(bx - ay) = 3b - 2a
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solve the system of equations by using the method of cross multiplication:
`x/6 + y/15 – 4 = 0, x/3 - y/12 – 19/4 = 0`
Solve 0.4x + 0.3y = 1.7; 0.7 x − 0.2y = 0.8
Find the values of x and y in the following rectangle [see figure].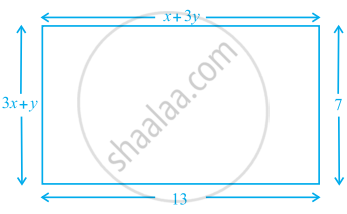
Determine, algebraically, the vertices of the triangle formed by the lines
3x – y = 2
2x – 3y = 2
x + 2y = 8
