Advertisements
Advertisements
प्रश्न
Solve the following :
Find the area enclosed between the circle x2 + y2 = 1 and the line x + y = 1, lying in the first quadrant.
उत्तर
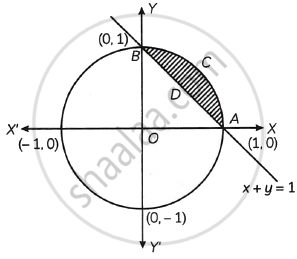
Required area = area of the region ACBDA
= (area of the region OACBO) – (area of the region OADBO) ...(1)
Now, area of the region OACBO
= area under the circle x2 + y2 = 1 between x = 0 and x = 1
= `int_0^1 y.dx`, where y2 = 1 – x2,
i.e. y = `sqrt(1 - x^2)`, as y > 0
= `int_0^1 sqrt(1 - x^2).dx`
= `[x/2 sqrt(1 - x^2) + 1/2 sin^-1 (x)]_0^1`
= `(1)/(2) sqrt(1 - 1) + 1/2 sin^-1 1- 0`
= `(1)/(2) xx pi/(2)`
= `pi/(4)` ...(2)
Area of the region OADBO = area under the line x + y = 1 between x = 0 and x = 1
= `int_0^1y.dx`, where y = 1 – x
= `int_0^1 (1 - x).dx`
= `[x - x^2/2]_0^1`
= `1 - (1)/(2) - 0`
= `(1)/(2)` ...(3)
Put the value of equation (2) and (3) in equation (1)
∴ Required area = `(pi/4 - 1/2)`sq units.
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the following curves, X-axis and the given lines: y = 2x, x = 0, x = 5
Find the area of the region bounded by the following curves, X-axis and the given lines: x = 2y, y = 0, y = 4
Find the area of the region bounded by the following curves, X-axis and the given lines : y = sin x, x = 0, x = `pi/(2)`
Find the area of the region bounded by the following curves, X-axis and the given lines: xy = 2, x = 1, x = 4
Find the area of the region bounded by the parabola y2 = 16x and its latus rectum.
Find the area of the region bounded by the parabola: y = 4 – x2 and the X-axis.
Find the area of the region included between: y2 = 4x, and y = x
Find the area of the region included between: y = x2 and the line y = 4x
Find the area of the region included between: y2 = 4ax and the line y = x
Find the area of the region included between y = x2 + 3 and the line y = x + 3.
Choose the correct option from the given alternatives :
The area bounded by the regional 1 ≤ x ≤ 5 and 2 ≤ y ≤ 5 is given by ______.
Choose the correct option from the given alternatives :
The area of the region enclosed by the curve y = `(1)/x`, and the lines x = e, x = e2 is given by
The area enclosed between the parabola y2 = 4x and line y = 2x is ______.
The area of the region bounded by y = cos x, Y-axis and the lines x = 0, x = 2π is ______.
Choose the correct option from the given alternatives :
The area bounded by the parabola y2 = 8x, the X-axis and the latus rectum is
Choose the correct option from the given alternatives :
The area under the curve y = `2sqrt(x)`, enclosed between the lines x = 0 and x = 1 is
Choose the correct option from the given alternatives :
The area of the region bounded by the ellipse `x^2/a^2 + y^2/b^2` = 1 is
Choose the correct option from the given alternatives :
The area enclosed between the curve y = cos 3x, 0 ≤ x ≤ `pi/(6)` and the X-axis is
Choose the correct option from the given alternatives :
The area bounded by y = `sqrt(x)` and the x = 2y + 3, X-axis in first quadrant is
Choose the correct option from the given alternatives :
The area bounded by the ellipse `x^2/a^2 y^2/b^2` = 1 and the line `x/a + y/b` = 1 is
Choose the correct option from the given alternatives :
The area enclosed between the two parabolas y2 = 4x and y = x is
Solve the following :
Find the area of the region bounded by the following curve, the X-axis and the given lines : 0 ≤ x ≤ 5, 0 ≤ y ≤ 2
Solve the following :
Find the area of the region bounded by the following curve, the X-axis and the given lines : y = sin x, x = 0, x = π
Solve the following :
Find the area of the region bounded by the following curve, the X-axis and the given lines : y = sin x, x = 0, x = `pi/(3)`
Solve the following :
Find the area of the region lying between the parabolas : y2 = x and x2 = y.
Solve the following :
Find the area of the region bounded by the straight line 2y = 5x + 7, X-axis and x = 2, x = 5.
Solve the following :
Find the area of the region bounded by the curve y = 4x2, Y-axis and the lines y = 1, y = 4.
The area of the region bounded by the curve y = sinx, X-axis and the lines x = 0, x = 4π is ______ sq.units
The area bounded by the parabola y2 = x along the X-axis and the lines x = 0, x = 2 is ______ sq.units
The area enclosed by the line 2x + 3y = 6 along X-axis and the lines x = 0, x = 3 is ______ sq.units
Find the area bounded by the curve y2 = 36x, the line x = 2 in first quadrant
Find the area of the region bounded by the parabola y2 = 32x and its Latus rectum in first quadrant
Using integration, find the area of the region bounded by the line 2y + x = 8 , X−axis and the lines x = 2 and x = 4
Find the area of the region bounded by the curve y = sin x, the X−axis and the given lines x = − π, x = π
Find the area of the region bounded by the curves y2 = 4ax and x2 = 4ay
Find the area of the sector bounded by the circle x2+ y2 = 16, and the line y = x in the first quadrant
Find the area of the region bounded by the curve y2 = 4x, the X-axis and the lines x = 1, x = 4 for y ≥ 0.
Find the area of the region bounded by the curve y = x2 and the line y = 4.
Find the area common to the parabola y2 = x – 3 and the line x = 5.
Find the area bounded by the lines y = 5x – 10, X-axis and x = 5.
Find the area of the region bounded by the curve y = x2, and the lines x = 1, x = 2, and y = 0.
