Advertisements
Advertisements
प्रश्न
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
उत्तर
Since the decision variables, x1 and x2 are non-negative, the solution lies in the I quadrant of the plane.
Consider the equations
x1 + x2 = 6
| x1 | 0 | 6 |
| x2 | 6 | 0 |
x1 = 4 is a line parallel to x2-axis at a distance of 4 units.
x2 = 5 is a line parallel to x1-axis at a distance of 5 units.
The feasible region is OABCD and its co-ordinates are O(0, 0) A(4, 0) D(5, 0) and B is the point of intersection of the lines x1 + x2 = 6 and x1 = 4
Also C is the point of intersection of the lines x1 + x2 = 6 and x2 = 5
Verification of B:
x1 + x2 = 6 and x1 = 4
4 + x2 = 6
x2 = 2
∴ B is (4, 2)
Verification of C:
x1 + x2 = 6 and x2 = 5
x1 + 5 = 6
x1 = 1
∴ C is (1, 5)
| Corner points | Z = 3x1 + 5x2 |
| O(0, 0) | 0 |
| A(4, 0) | 12 |
| B(4, 2) | 22 |
| C(1, 5) | 26 |
| D(5, 0) | 15 |
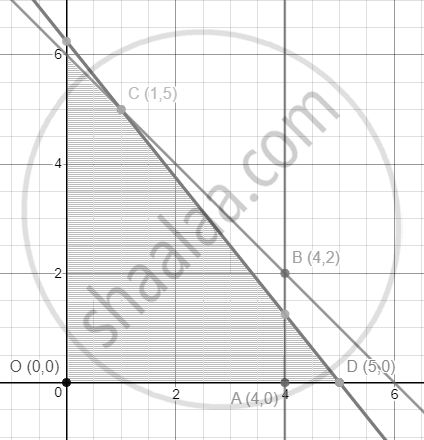
Maximum of Z occurs at C(1, 5)
∴ The solution is x1 = 1, x2 = 5 and Zmax = 26.
APPEARS IN
संबंधित प्रश्न
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 in magazines A and B per copy. These are processed on three Machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II, and 2 hours on machine III. Magazine B requires 3 hours on machine I, 2 hours on machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, and 60 hours per week respectively. Formulate the LPP to determine weekly production of magazines A and B, so that the total profit is maximum.
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
A firm manufactures two products A and B on which profit earned per unit ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. The product A requires one minute of processing time on M1 and two minutes of processing time on M2, B requires one minute of processing time on M1 and one minute of processing time on M2. Machine M1 is available for use for 450 minutes while M2 is available for 600 minutes during any working day. Find the number of units of product A and B to be manufactured to get the maximum profit.
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Minimize z = 7x + y subjected to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
The variables involved in LPP are called ______
Constraints are always in the form of ______ or ______.
Find graphical solution for the following system of linear in equation:
x + 2y ≥ 4, 2x - y ≤ 6
