Advertisements
Advertisements
Question
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Solution
Since the decision variables, x1 and x2 are non-negative, the solution lies in the I quadrant of the plane.
Consider the equations
x1 + x2 = 6
| x1 | 0 | 6 |
| x2 | 6 | 0 |
x1 = 4 is a line parallel to x2-axis at a distance of 4 units.
x2 = 5 is a line parallel to x1-axis at a distance of 5 units.
The feasible region is OABCD and its co-ordinates are O(0, 0) A(4, 0) D(5, 0) and B is the point of intersection of the lines x1 + x2 = 6 and x1 = 4
Also C is the point of intersection of the lines x1 + x2 = 6 and x2 = 5
Verification of B:
x1 + x2 = 6 and x1 = 4
4 + x2 = 6
x2 = 2
∴ B is (4, 2)
Verification of C:
x1 + x2 = 6 and x2 = 5
x1 + 5 = 6
x1 = 1
∴ C is (1, 5)
| Corner points | Z = 3x1 + 5x2 |
| O(0, 0) | 0 |
| A(4, 0) | 12 |
| B(4, 2) | 22 |
| C(1, 5) | 26 |
| D(5, 0) | 15 |
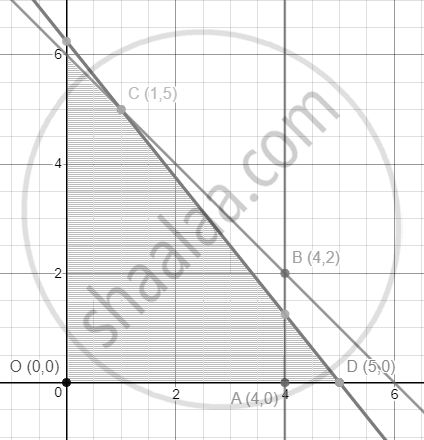
Maximum of Z occurs at C(1, 5)
∴ The solution is x1 = 1, x2 = 5 and Zmax = 26.
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Find the feasible solution of the following inequation:
3x + 4y ≥ 12, 4x + 7y ≤ 28, y ≥ 1, x ≥ 0.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following LPP by graphical method:
Minimize z = 8x + 10y, subject to 2x + y ≥ 7, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0.
Sketch the graph of the following inequation in XOY co-ordinate system:
|x + 5| ≤ y
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
The corner points of the feasible region are (0, 0), (2, 0), `(12/7, 3/7)` and (0,1) then the point of maximum z = 7x + y
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
State whether the following statement is True or False:
Objective function of LPP is a relation between the decision variables
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
