Advertisements
Advertisements
Question
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
Solution
Since the decision variables, x1 and x2 are non-negative, the solution lies in the I quadrant of the plane.
Consider the equations
x1 + x2 = 50
| x1 | 0 | 50 |
| x2 | 50 | 0 |
3x1 + x2 = 90
| x1 | 0 | 30 |
| x2 | 90 | 0 |
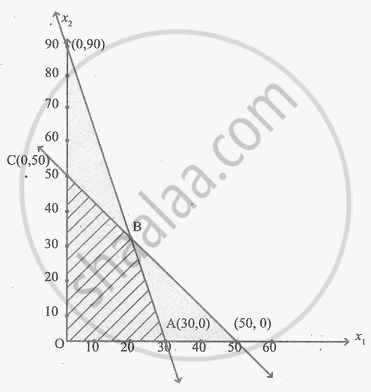
The feasible region is OABC and its co-ordinates are O(0, 0) A(30, 0) C(0, 50) and B is the point of intersection of the lines
x1 + x2 = 50 ..........(1)
3x1 + x2 = 90 .........(2)
Verification of B:
x1 + x2 = 50 ..........(1)
3x1 + x2 = 90 .........(2)
− − −
− 2x1 = − 40
x1 = 20
From (1), 20 + x2 = 50
x2 = 30
∴ B is (20, 30)
| Corner points | Z = 60x1 + 15x2 |
| O(0, 0) | 0 |
| A(30, 0) | 1800 |
| B(20, 30) | 1650 |
| C(0, 50) | 7500 |
Maximum value occurs at C(0, 50)
∴ The solution is x1 = 0, x2 = 50 and Zmax = 7500.
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
Solve each of the following inequations graphically using XY-plane:
5y - 12 ≥ 0
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each units of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufactured per month to maximize profit? How much is the maximum profit?
Choose the correct alternative :
The half plane represented by 3x + 2y ≤ 0 constraints the point.
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Minimize z = 7x + y subjected to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
The maximum value of Z = 3x + 5y, subject to 3x + 2y ≤ 18, x ≤ a, y ≤ 6, x, y ≥ 0 is ______.
The optimal value of the objective function is attained at the ______ of feasible region.
