Advertisements
Advertisements
प्रश्न
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
उत्तर
Since the decision variables, x1 and x2 are non-negative, the solution lies in the I quadrant of the plane.
Consider the equations
x1 + x2 = 50
| x1 | 0 | 50 |
| x2 | 50 | 0 |
3x1 + x2 = 90
| x1 | 0 | 30 |
| x2 | 90 | 0 |
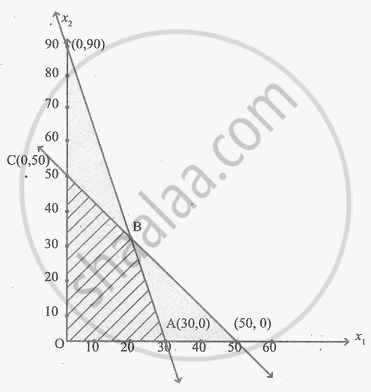
The feasible region is OABC and its co-ordinates are O(0, 0) A(30, 0) C(0, 50) and B is the point of intersection of the lines
x1 + x2 = 50 ..........(1)
3x1 + x2 = 90 .........(2)
Verification of B:
x1 + x2 = 50 ..........(1)
3x1 + x2 = 90 .........(2)
− − −
− 2x1 = − 40
x1 = 20
From (1), 20 + x2 = 50
x2 = 30
∴ B is (20, 30)
| Corner points | Z = 60x1 + 15x2 |
| O(0, 0) | 0 |
| A(30, 0) | 1800 |
| B(20, 30) | 1650 |
| C(0, 50) | 7500 |
Maximum value occurs at C(0, 50)
∴ The solution is x1 = 0, x2 = 50 and Zmax = 7500.
APPEARS IN
संबंधित प्रश्न
A company manufactures two types of chemicals Aand B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.
| Chemical→ | A | B | Availability |
| Raw Material ↓ | |||
| P | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company gets a maximum profit? Formulate the problem as LPP to maximize profit.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. If maximum availability of Machine M1 is 10 hours and that of Machine M2 is 12 hours, then formulate the L.P.P. to maximize the profit.
Solve the following L.P.P. by graphical method:
Maximize: Z = 4x + 6y
Subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Choose the correct alternative :
The corner points of the feasible region are (0, 0), (2, 0), `(12/7, 3/7)` and (0,1) then the point of maximum z = 7x + y
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
x − y ≤ 1, x − y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x + y. It is solvable for finding optimum value of z? Justify?
Choose the correct alternative:
The feasible region is
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
In the given graph the coordinates of M1 are

