Advertisements
Advertisements
प्रश्न
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
उत्तर
Since the decision variables, x1 and x2 are non-negative, the solution lies in the I quadrant of the plane.
Consider the equations
x1 + x2 = 50
| x1 | 0 | 50 |
| x2 | 50 | 0 |
3x1 + x2 = 90
| x1 | 0 | 30 |
| x2 | 90 | 0 |
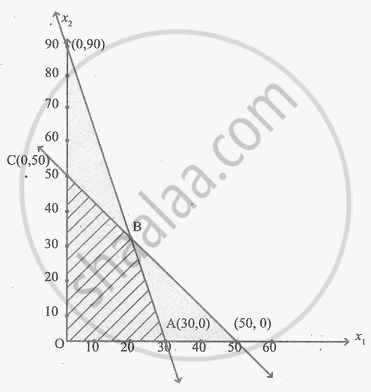
The feasible region is OABC and its co-ordinates are O(0, 0) A(30, 0) C(0, 50) and B is the point of intersection of the lines
x1 + x2 = 50 ..........(1)
3x1 + x2 = 90 .........(2)
Verification of B:
x1 + x2 = 50 ..........(1)
3x1 + x2 = 90 .........(2)
− − −
− 2x1 = − 40
x1 = 20
From (1), 20 + x2 = 50
x2 = 30
∴ B is (20, 30)
| Corner points | Z = 60x1 + 15x2 |
| O(0, 0) | 0 |
| A(30, 0) | 1800 |
| B(20, 30) | 1650 |
| C(0, 50) | 7500 |
Maximum value occurs at C(0, 50)
∴ The solution is x1 = 0, x2 = 50 and Zmax = 7500.
APPEARS IN
संबंधित प्रश्न
Which of the following statements is correct?
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
A furniture dealer deals in tables and chairs. He has ₹ 1,50,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 1500 and a chair ₹ 750. Construct the inequations and find the feasible solution.
Fill in the blank :
The optimal value of the objective function is attained at the _______ points of feasible region.
A train carries at least twice as many first class passengers (y) as second class passengers (x) The constraint is given by_______
Maximize z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
A solution which maximizes or minimizes the given LPP is called
A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
