Advertisements
Advertisements
प्रश्न
A furniture dealer deals in tables and chairs. He has ₹ 1,50,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 1500 and a chair ₹ 750. Construct the inequations and find the feasible solution.
उत्तर
Let x be the number of tables and y be the number of chairs. Then x ≥ 0, y ≥ 0.
The dealer has a space to store at most 60 pieces.
∴ x + y ≤ 60
Since, the cost of each table is ₹ 1500 and that of each chair is ₹ 750, the total cost of x tables and y chairs is 1500x + 750y. Since the dealer has ₹ 1,50,000 to invest, 1500x + 750y ≤ 1,50,000 = 2x + y ≤ 200
Hence the system of inequations are
x + y ≤ 60, 2x + y ≤ 200
First we draw the lines AB and CD whose equations are
x + y = 60 and 2x + y = 200, x ≥ 0, y ≥ 0 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | x + y = 60 | A(60,0) | B(0,60) | ≤ | origin side of line AB |
| CD | 2x + y = 200 | C(100,0) | D(0,200) | ≤ | origin side of line CD |
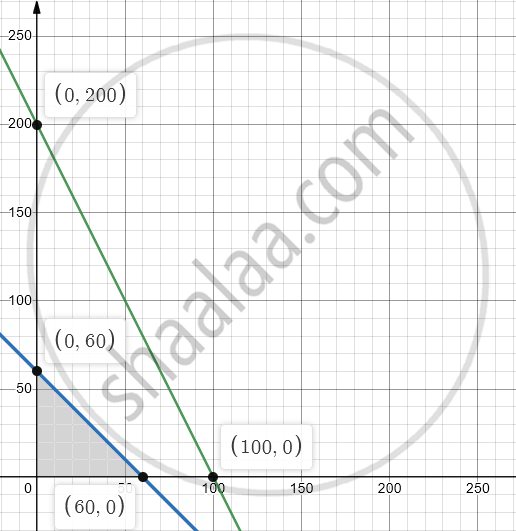
The feasible solution is shaded in the graph.
APPEARS IN
संबंधित प्रश्न
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14. 22 and 1 units of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients:
| Fodder → | Fodder 1 | Fodder 2 |
| Nutrient ↓ | ||
| Nutrients A | 2 | 1 |
| Nutrients B | 2 | 3 |
| Nutrients C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 ₹ 2. Formulate the LPP to minimize the cost.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
A doctor has prescribed two different units of foods A and B to form a weekly diet for a sick person. The minimum requirements of fats, carbohydrates and proteins are 18, 28, 14 units respectively. One unit of food A has 4 units of fat, 14 units of carbohydrates and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the LPP, so that the sick person’s diet meets the requirements at a minimum cost.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following LPP by graphical method:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solve the following LPP by graphical method:
Minimize z = 8x + 10y, subject to 2x + y ≥ 7, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0.
The maximum value of z = 5x + 3y subject to the constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x, y ≥ 0 is ______.
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
The point of which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x, ≥ 0, y ≥ 0 is is obtained at ______.
Of all the points of the feasible region, the optimal value of z obtained at the point lies ______.
Solution of LPP to minimize z = 2x + 3y, such that x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is ______.
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are ______.
Solve each of the following inequations graphically using XY-plane:
5y - 12 ≥ 0
Solve each of the following inequations graphically using XY-plane:
y ≤ - 3.5
Sketch the graph of the following inequation in XOY co-ordinate system:
|x + 5| ≤ y
Solve the following LPP:
Maximize z =60x + 50y subject to
x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0.
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each units of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufactured per month to maximize profit? How much is the maximum profit?
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to machine shop for finishing. The number of man hours of labour required in each shop for production of A and B and the number of man hours available for the firm are as follows:
| Gadgets | Foundry | Machine Shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hours) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per unit. Formulate the L.P.P. to have maximum profit.
In a cattle breeding firm, it is prescribed that the food ration for one animal must contain 14, 22, and 1 unit of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit weight of these two contains the following amounts of these three nutrients:
| Nutrient\Fodder | Fodder 1 | Fodder2 |
| Nutrient A | 2 | 1 |
| Nutrient B | 2 | 3 |
| Nutrient C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder ₹ 2 per unit. Formulate the L.P.P. to minimize the cost.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
The half plane represented by 4x + 3y ≥ 14 contains the point
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
Maximize z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Constraints are always in the form of ______ or ______.
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
Maximize: z = 3x1 + 4x2 subject to 2x1 + x2 ≤ 40, 2x1 + 5x2 ≤ 180, x1, x2 ≥ 0. In the LPP, which one of the following is feasible comer point?
Given an L.P.P maximize Z = 2x1 + 3x2 subject to the constrains x1 + x2 ≤ 1, 5x1 + 5x2 ≥ 0 and x1 ≥ 0, x2 ≥ 0 using graphical method, we observe
A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
The maximum value of Z = 3x + 5y, subject to 3x + 2y ≤ 18, x ≤ a, y ≤ 6, x, y ≥ 0 is ______.
The LPP to maximize Z = x + y, subject to x + y ≤ 1, 2x + 2y ≥ 6, x ≥ 0, y ≥ 0 has ________.
The set of feasible solutions of LPP is a ______.
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
Two kinds of foods A and B are being considered to form a weekly diet. The minimum weekly requirements of fats, Carbohydrates and proteins are 12, 16 and 15 units respectively. One kg of food A has 2, 8 and 5 units respectively of these ingredients and one kg of food B has 6, 2 and 3 units respectively. The price of food A is Rs. 4 per kg and that of food B is Rs. 3 per kg. Formulate the L.P.P. and find the minimum cost.
