Advertisements
Advertisements
प्रश्न
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
उत्तर
Given that 3x1 + x2 ≤ 9
Let 3x1 + x2 = 9
| x1 | 0 | 3 |
| x2 | 9 | 0 |
Also given that x1 + 2x2 ≤ 8]
Let x1 + 2x2 = 8
| x1 | 0 | 8 |
| x2 | 4 | 0 |
3x1 + x2 = 9 ………(1)
x1 + 2x2 = 8 ……..(2)
6x1 + 2x2 = 18 ……..(3) [Multiply by 2 for eq. (1)]
− 5x1 = − 10
x1 = 2
x1 = 2 substitute in (1)
3(2) + x2 = 9
x2 = 3
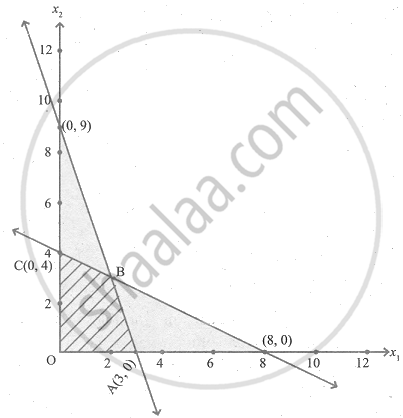
The feasible region satisfying all the conditions is OABC.
The co-ordinates of the corner points are O(0, 0), A(3, 0), B(2, 3), C(0, 4)
| Corner points | Z = 40x1 + 50x2 |
| O(0, 0) | 0 |
| A(3, 0) | 120 |
| B(2, 3) | 40 × 2 + 50 × 3 = 80 + 150 = 230 |
| C(0, 4) | 200 |
The maximum value of Z occurs at B(2, 3).
∴ The optimal solution is x1 = 2, x2 = 3 and Zmax = 230
APPEARS IN
संबंधित प्रश्न
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
Solve the following LPP by graphical method:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
State whether the following is True or False :
Saina wants to invest at most ₹ 24000 in bonds and fixed deposits. Mathematically this constraints is written as x + y ≤ 24000 where x is investment in bond and y is in fixed deposits.
The point of which the maximum value of z = x + y subject to constraints x + 2y ≤ 70, 2x + y ≤ 90, x ≥ 0, y ≥ 0 is obtained at
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Choose the correct alternative:
The feasible region is
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solution which satisfy all constraints is called ______ solution.
Sketch the graph of the following inequation in XOY co-ordinate system.
2y - 5x ≥ 0
