Advertisements
Advertisements
Question
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
Solution
Given that 3x1 + x2 ≤ 9
Let 3x1 + x2 = 9
| x1 | 0 | 3 |
| x2 | 9 | 0 |
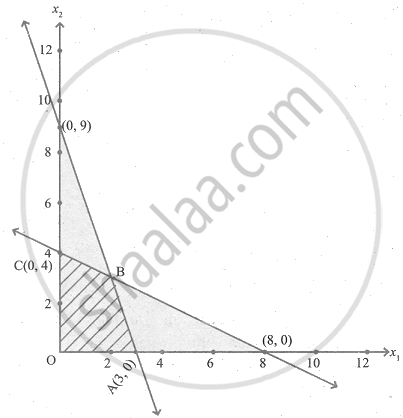
Also given that x1 + 2x2 ≤ 8]
Let x1 + 2x2 = 8
| x1 | 0 | 8 |
| x2 | 4 | 0 |
3x1 + x2 = 9 ………(1)
x1 + 2x2 = 8 ……..(2)
6x1 + 2x2 = 18 ……..(3) [Multiply by 2 for eq. (1)]
− 5x1 = − 10
x1 = 2
x1 = 2 substitute in (1)
3(2) + x2 = 9
x2 = 3
The feasible region satisfying all the conditions is OABC.
The co-ordinates of the corner points are O(0, 0), A(3, 0), B(2, 3), C(0, 4)
| Corner points | Z = 40x1 + 50x2 |
| O(0, 0) | 0 |
| A(3, 0) | 120 |
| B(2, 3) | 40 × 2 + 50 × 3 = 80 + 150 = 230 |
| C(0, 4) | 200 |
The maximum value of Z occurs at B(2, 3).
∴ The optimal solution is x1 = 2, x2 = 3 and Zmax = 230
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
If John drives a car at a speed of 60 km/hour, he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 km/hour, the cost of petrol increases ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
Solve each of the following inequations graphically using XY-plane:
y ≤ - 3.5
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. If maximum availability of Machine M1 is 10 hours and that of Machine M2 is 12 hours, then formulate the L.P.P. to maximize the profit.
A train carries at least twice as many first class passengers (y) as second class passengers (x) The constraint is given by_______
A company manufactures two models of voltage stabilizers viz., ordinary and auto-cut. All components of the stabilizers are purchased from outside sources, assembly and testing is carried out at the company’s own works. The assembly and testing time required for the two models are 0.8 hours each for ordinary and 1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is available per week. The market for the two models has been surveyed which suggests a maximum weekly sale of 600 units of ordinary and 400 units of auto-cut. Profit per unit for ordinary and auto-cut models has been estimated at ₹ 100 and ₹ 150 respectively. Formulate the linear programming problem.
The set of feasible solutions of LPP is a ______.
