Advertisements
Advertisements
Question
Solve each of the following inequations graphically using XY-plane:
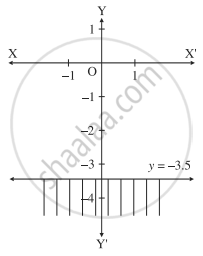
y ≤ - 3.5
Solution
Consider the line whose equation is y ≤ - 3.5 i.e. y = - 3.5
This represents a line parallel to X-axis passing3through the point `(0, - 3.5)`
Draw the line y = - 3.5
To find the solution set, we have to check the position of the origin (0, 0).
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line y = - 3.5 and the non-origin side of the line which is shaded in the graph.
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
Find the feasible solution of the following inequation:
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
A furniture dealer deals in tables and chairs. He has ₹ 1,50,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 1500 and a chair ₹ 750. Construct the inequations and find the feasible solution.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B per unit and the number of man-hours available for the firm is as follows :
| Gadgets | Foundry | Machine shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hour) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 in magazines A and B per copy. These are processed on three Machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II, and 2 hours on machine III. Magazine B requires 3 hours on machine I, 2 hours on machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, and 60 hours per week respectively. Formulate the LPP to determine weekly production of magazines A and B, so that the total profit is maximum.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
Solve the following LPP by graphical method:
Minimize z = 8x + 10y, subject to 2x + y ≥ 7, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0.
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
Objective function of LPP is ______.
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
Solution of LPP to minimize z = 2x + 3y, such that x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is ______.
The half-plane represented by 3x + 2y < 8 contains the point ______.
Fill in the blank :
The optimal value of the objective function is attained at the _______ points of feasible region.
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
Maximize z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
Choose the correct alternative:
Z = 9x + 13y subjected to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, 0 ≤ x, y was found to be maximum at the point
State whether the following statement is True or False:
LPP is related to efficient use of limited resources
Constraints are always in the form of ______ or ______.
A company manufactures two models of voltage stabilizers viz., ordinary and auto-cut. All components of the stabilizers are purchased from outside sources, assembly and testing is carried out at the company’s own works. The assembly and testing time required for the two models are 0.8 hours each for ordinary and 1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is available per week. The market for the two models has been surveyed which suggests a maximum weekly sale of 600 units of ordinary and 400 units of auto-cut. Profit per unit for ordinary and auto-cut models has been estimated at ₹ 100 and ₹ 150 respectively. Formulate the linear programming problem.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Maximize: z = 3x1 + 4x2 subject to 2x1 + x2 ≤ 40, 2x1 + 5x2 ≤ 180, x1, x2 ≥ 0. In the LPP, which one of the following is feasible comer point?
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
The maximum value of Z = 3x + 5y, subject to 3x + 2y ≤ 18, x ≤ a, y ≤ 6, x, y ≥ 0 is ______.
The values of θ satisfying sin7θ = sin4θ - sinθ and 0 < θ < `pi/2` are ______
Which of the following can be considered as the objective function of a linear programming problem?
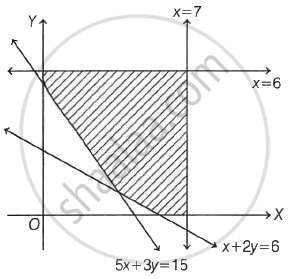
For the following shaded region, the linear constraint are:
Sketch the graph of the following inequation in XOY co-ordinate system.
x + y ≤ 0
Sketch the graph of the following inequation in XOY co-ordinate system.
2y - 5x ≥ 0
Find graphical solution for the following system of linear in equation:
x + 2y ≥ 4, 2x - y ≤ 6
