Advertisements
Advertisements
Question
The half-plane represented by 3x + 2y < 8 contains the point ______.
Options
`(1, 5/2)`
(2, 1)
(0, 0)
(5, 1)
Solution
The half-plane represented by 3x + 2y < 8 contains the point (0, 0).
Notes
The answer in the textbook is incorrect.
APPEARS IN
RELATED QUESTIONS
Which of the following statements is correct?
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below:
| Fertilizers→ | F1 | F2 | Availability |
| Raw Material ↓ | |||
| A | 2 | 3 | 40 |
| B | 1 | 4 | 70 |
By selling one unit of F1 and one unit of F2, the company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as LPP to maximize the profit.
A doctor has prescribed two different units of foods A and B to form a weekly diet for a sick person. The minimum requirements of fats, carbohydrates and proteins are 18, 28, 14 units respectively. One unit of food A has 4 units of fat, 14 units of carbohydrates and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the LPP, so that the sick person’s diet meets the requirements at a minimum cost.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Minimize z = 6x + 2y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Which of the following is correct?
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
Solve each of the following inequations graphically using XY-plane:
- 11x - 55 ≤ 0
Solve each of the following inequations graphically using XY-plane:
y ≤ - 3.5
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
A company produces mixers and food processors. Profit on selling one mixer and one food processor is Rs 2,000 and Rs 3,000 respectively. Both the products are processed through three machines A, B, C. The time required in hours for each product and total time available in hours per week on each machine arc as follows:
| Machine | Mixer | Food Processor | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced in order to maximize the profit?
A chemical company produces a chemical containing three basic elements A, B, C, so that it has at least 16 litres of A, 24 litres of B and 18 litres of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 litres of A, 12 litres of B and 2 litres of C. Each unit of compound II has 2 litres of A, 2 litres of B and 6 litres of C. The cost per unit of compound I is ₹ 800 and that of compound II is ₹ 640. Formulate the problems as LPP and solve it to minimize the cost.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
Of all the points of the feasible region the optimal value of z is obtained at a point
State whether the following is True or False :
Saina wants to invest at most ₹ 24000 in bonds and fixed deposits. Mathematically this constraints is written as x + y ≤ 24000 where x is investment in bond and y is in fixed deposits.
Maximize z = 10x + 25y subject to x + y ≤ 5, 0 ≤ x ≤ 3, 0 ≤ y ≤ 3
x − y ≤ 1, x − y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x + y. It is solvable for finding optimum value of z? Justify?
Choose the correct alternative:
The feasible region is
The variables involved in LPP are called ______
A company produces two types of pens A and B. Pen A is of superior quality and pen B is of lower quality. Profits on pens A and B are ₹ 5 and ₹ 3 per pen respectively. Raw materials required for each pen A is twice as that of pen B. The supply of raw material is sufficient only for 1000 pens per day. Pen A requires a special clip and only 400 such clips are available per day. For pen B, only 700 clips are available per day. Formulate this problem as a linear programming problem.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
The maximum value of the objective function Z = 3x + 5y subject to the constraints x ≥ 0, y ≥ 0 and 2x + 5y ≤ 10 is
A firm manufactures pills in two sizes A and B. Size A contains 2 mgs of aspirin, 5 mgs of bicarbonate and 1 mg of codeine. Size B contains 1 mg. of aspirin, 8 mgs. of bicarbonate and 6 mgs. of codeine. It is found by users that it requires at least 12 mgs. of aspirin, 74 mgs. of bicarbonate and 24 mgs. of codeine for providing immediate relief. It is required to determine the least number of pills a patient should take to get immediate relief. Formulate the problem as a standard LLP.
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
The optimal value of the objective function is attained at the ______ of feasible region.
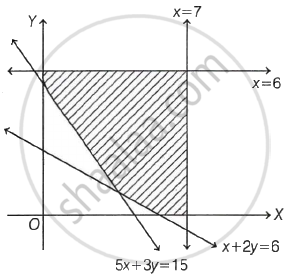
For the following shaded region, the linear constraint are:
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y Subject to: x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
Two kinds of foods A and B are being considered to form a weekly diet. The minimum weekly requirements of fats, Carbohydrates and proteins are 12, 16 and 15 units respectively. One kg of food A has 2, 8 and 5 units respectively of these ingredients and one kg of food B has 6, 2 and 3 units respectively. The price of food A is Rs. 4 per kg and that of food B is Rs. 3 per kg. Formulate the L.P.P. and find the minimum cost.
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
