Advertisements
Advertisements
Question
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solution
Given that 30x1 + 20x2 ≤ 300
Let 30x1 + 20x2 = 300
Therefore 3x1 + 2x2 = 30
| x1 | 0 | 10 |
| x2 | 15 | 0 |
Also given that 5x1 + 10x2 ≤ 110
Let 5x1 + 10x2 = 110
x1 + 2x2 = 22
| x1 | 0 | 22 |
| x2 | 11 | 0 |
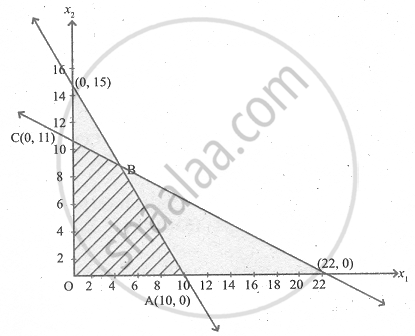
To get point of intersection, (i.e., the to get co-ordinates of B)
3x1 + 2x2 = 30 …….(1)
x1 + 2x2 = 22 ……..(2)
2x1 = 8 ......[Equation (1) – (2)]
x1 = 4
x1 = 4 substitute in (1),
x1 + 2x2 = 22
4 + 2x2 = 22
2x2 = 18
x2 = 9
i.e., B is (4, 9)
The feasible region satisfying all the given conditions is OABC.
The co-ordinates of the points are O(0, 0), A(10, 0), B(4, 9), C(0, 11).
| Corner points | Z = 6x1 + 8x2 |
| O(0, 0) | 0 |
| A(10, 0) | 60 |
| B(4, 9) | 6 × 4 + 8 × 9 = 96 |
| C(0, 11) | 88 |
The maximum value of Z occurs at B(4, 9).
∴ The optimal solution is x1 = 4, x2 = 9 and Zmax = 96
APPEARS IN
RELATED QUESTIONS
Solve the following LPP by graphical method:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solution of LPP to minimize z = 2x + 3y, such that x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is ______.
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
Solve the following LPP:
Minimize z = 4x + 2y
Subject to 3x + y ≥ 27, x + y ≥ 21, x + 2y ≥ 30, x ≥ 0, y ≥ 0
A firm manufactures two products A and B on which profit earned per unit ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. The product A requires one minute of processing time on M1 and two minutes of processing time on M2, B requires one minute of processing time on M1 and one minute of processing time on M2. Machine M1 is available for use for 450 minutes while M2 is available for 600 minutes during any working day. Find the number of units of product A and B to be manufactured to get the maximum profit.
State whether the following statement is True or False:
Objective function of LPP is a relation between the decision variables
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
The maximum value of Z = 3x + 5y, subject to 3x + 2y ≤ 18, x ≤ a, y ≤ 6, x, y ≥ 0 is ______.
The values of θ satisfying sin7θ = sin4θ - sinθ and 0 < θ < `pi/2` are ______
For the following shaded region, the linear constraint are: