Advertisements
Advertisements
Question
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
Solution
Given that 960x1 + 640x2 ≤ 15360
Let 960x1 + 640x2 = 15360
3x1 + 2x2 = 48
| x1 | 0 | 16 |
| x2 | 24 | 0 |
Also given that x1 + x2 ≤ 20
Let x1 + x2 = 20
| x1 | 0 | 20 |
| x2 | 20 | 0 |
To get point of intersection
3x1 + 2x2 = 48 …..(1)
x1 + x2 = 20 ……(2)
− 2x1 – 2x2 = – 40 …..(3) ......[Equation (2) × –2]
x1 = 8 .....[Adding equation (1) and (3)]
x1 = 8 substitute in (2),
8 + x2 = 20
x2 = 12
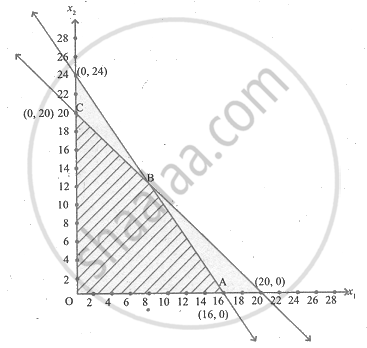
The feasible region satisfying all the given conditions is OABC.
The co-ordinates of the comer points are O(0, 0), A(16, 0), B(8,12) and C(0, 16).
| Corner points | Z = 22x1 + 18x2 |
| O(0, 0) | 0 |
| A(16, 0) | 352 |
| B(8, 12) | 392 |
| C(0, 20) | 360 |
The maximum value of Z occurs at B(8, 12).
∴ The optimal solution is x1 = 8, x2 = 12 and Zmax = 392
APPEARS IN
RELATED QUESTIONS
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are ______.
Solve the following LPP:
Maximize z = 4x1 + 3x2 subject to
3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0.
A company produces mixers and food processors. Profit on selling one mixer and one food processor is Rs 2,000 and Rs 3,000 respectively. Both the products are processed through three machines A, B, C. The time required in hours for each product and total time available in hours per week on each machine arc as follows:
| Machine | Mixer | Food Processor | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced in order to maximize the profit?
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the Linear programming problem to maximize the profit.
Solve the following L.P.P. by graphical method:
Maximize: Z = 4x + 6y
Subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
State whether the following is True or False :
The point (1, 2) is not a vertex of the feasible region bounded by 2x + 3y ≤ 6, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Maximize z = 5x + 2y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
In the given graph the coordinates of M1 are

