Advertisements
Advertisements
प्रश्न
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
उत्तर
Given that 960x1 + 640x2 ≤ 15360
Let 960x1 + 640x2 = 15360
3x1 + 2x2 = 48
| x1 | 0 | 16 |
| x2 | 24 | 0 |
Also given that x1 + x2 ≤ 20
Let x1 + x2 = 20
| x1 | 0 | 20 |
| x2 | 20 | 0 |
To get point of intersection
3x1 + 2x2 = 48 …..(1)
x1 + x2 = 20 ……(2)
− 2x1 – 2x2 = – 40 …..(3) ......[Equation (2) × –2]
x1 = 8 .....[Adding equation (1) and (3)]
x1 = 8 substitute in (2),
8 + x2 = 20
x2 = 12
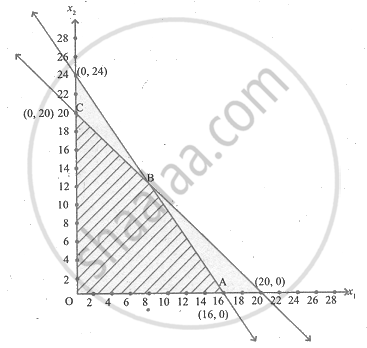
The feasible region satisfying all the given conditions is OABC.
The co-ordinates of the comer points are O(0, 0), A(16, 0), B(8,12) and C(0, 16).
| Corner points | Z = 22x1 + 18x2 |
| O(0, 0) | 0 |
| A(16, 0) | 352 |
| B(8, 12) | 392 |
| C(0, 20) | 360 |
The maximum value of Z occurs at B(8, 12).
∴ The optimal solution is x1 = 8, x2 = 12 and Zmax = 392
APPEARS IN
संबंधित प्रश्न
A company manufactures two types of chemicals Aand B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.
| Chemical→ | A | B | Availability |
| Raw Material ↓ | |||
| P | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company gets a maximum profit? Formulate the problem as LPP to maximize profit.
The point of which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x, ≥ 0, y ≥ 0 is is obtained at ______.
Solve the following LPP:
Maximize z = 2x + 3y subject to x - y ≥ 3, x ≥ 0, y ≥ 0.
Solve each of the following inequations graphically using XY-plane:
5y - 12 ≥ 0
Solve the following LPP:
Maximize z = 4x1 + 3x2 subject to
3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0.
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each units of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufactured per month to maximize profit? How much is the maximum profit?
Choose the correct alternative :
Feasible region; the set of points which satify.
The variables involved in LPP are called ______
Given an L.P.P maximize Z = 2x1 + 3x2 subject to the constrains x1 + x2 ≤ 1, 5x1 + 5x2 ≥ 0 and x1 ≥ 0, x2 ≥ 0 using graphical method, we observe
