Advertisements
Advertisements
प्रश्न
Solve the following linear programming problems by graphical method.
Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 ≥ 6; x1 + 4x2 ≥ 12 and x1, x2 ≥ 0.
उत्तर
Given that 5x1 + x2 ≥ 10
Let 5x1 + x2 = 10
| x1 | 0 | 2 |
| x2 | 10 | 0 |
Also given that x1 + x2 ≥ 6
Let x1 + x2 = 6
| x1 | 0 | 6 |
| x2 | 6 | 0 |
Also given that x1 + 4x2 ≥ 12
Let x1 + 4x2 = 12
| x1 | 0 | 12 |
| x2 | 3 | 0 |
To get B
5x1 + x2 = 10 ……..(1)
x1 + x2 = 6 ………(2)
4x1 = 4 ......[Equation (1) – (2)]
x1 = 1
x = 1 substitute in (2)
x1 + x2 = 6
1 + x2 = 6
x2 = 5
∴ B is (1, 5)
To get C
x1 + x2 = 6
x1 + 4x2 = 12
− 3x2 = − 6 ..........[Equation (1) – (2)]
x2 = 2
x2 = 2 substitute in (2) we get,
x1 + x2 = 6
x1 = 4
∴ C is (4, 2)
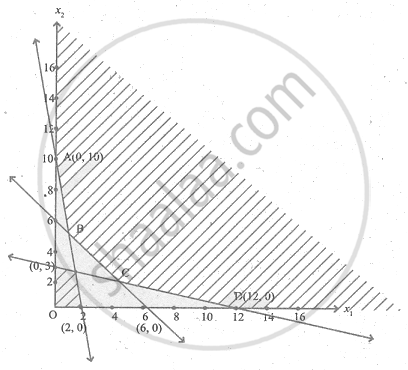
The feasible region satisfying all the conditions is ABCD.
The coordinates of the comer points are A(0, 10), B(1, 5), C(4, 2) and D(12, 0).
| Corner points | Z = 3x1 + 2x2 |
| A(0, 10) | 20 |
| B(1, 5) | 13 |
| C(4, 2) | 16 |
| D(12, 0) | 36 |
The minimum value of Z occours at B(1, 5).
∴ The optimal solution is x1 = 1, x2 = 5 and Zmin = 13
APPEARS IN
संबंधित प्रश्न
If the corner points of the feasible solution are (0, 0), (3, 0), (2, 1), `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
The half-plane represented by 4x + 3y >14 contains the point ______.
Solve the following LPP:
Maximize z = 4x1 + 3x2 subject to
3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. If maximum availability of Machine M1 is 10 hours and that of Machine M2 is 12 hours, then formulate the L.P.P. to maximize the profit.
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
Solve the following LPP:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
