Advertisements
Advertisements
प्रश्न
Solve the following linear programming problems by graphical method.
Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 ≥ 6; x1 + 4x2 ≥ 12 and x1, x2 ≥ 0.
उत्तर
Given that 5x1 + x2 ≥ 10
Let 5x1 + x2 = 10
| x1 | 0 | 2 |
| x2 | 10 | 0 |
Also given that x1 + x2 ≥ 6
Let x1 + x2 = 6
| x1 | 0 | 6 |
| x2 | 6 | 0 |
Also given that x1 + 4x2 ≥ 12
Let x1 + 4x2 = 12
| x1 | 0 | 12 |
| x2 | 3 | 0 |
To get B
5x1 + x2 = 10 ……..(1)
x1 + x2 = 6 ………(2)
4x1 = 4 ......[Equation (1) – (2)]
x1 = 1
x = 1 substitute in (2)
x1 + x2 = 6
1 + x2 = 6
x2 = 5
∴ B is (1, 5)
To get C
x1 + x2 = 6
x1 + 4x2 = 12
− 3x2 = − 6 ..........[Equation (1) – (2)]
x2 = 2
x2 = 2 substitute in (2) we get,
x1 + x2 = 6
x1 = 4
∴ C is (4, 2)
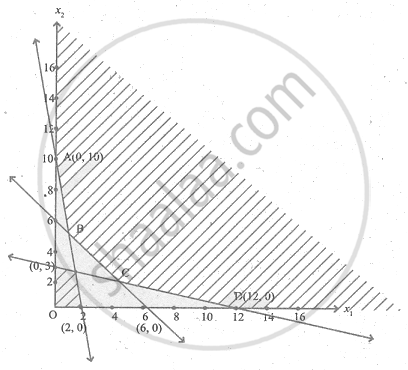
The feasible region satisfying all the conditions is ABCD.
The coordinates of the comer points are A(0, 10), B(1, 5), C(4, 2) and D(12, 0).
| Corner points | Z = 3x1 + 2x2 |
| A(0, 10) | 20 |
| B(1, 5) | 13 |
| C(4, 2) | 16 |
| D(12, 0) | 36 |
The minimum value of Z occours at B(1, 5).
∴ The optimal solution is x1 = 1, x2 = 5 and Zmin = 13
APPEARS IN
संबंधित प्रश्न
A doctor has prescribed two different units of foods A and B to form a weekly diet for a sick person. The minimum requirements of fats, carbohydrates and proteins are 18, 28, 14 units respectively. One unit of food A has 4 units of fat, 14 units of carbohydrates and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the LPP, so that the sick person’s diet meets the requirements at a minimum cost.
The half-plane represented by 3x + 2y < 8 contains the point ______.
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
Objective function of LPP is ______.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
A solution which maximizes or minimizes the given LPP is called
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
For the following shaded region, the linear constraint are:
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
