Advertisements
Advertisements
प्रश्न
Solve each of the following inequations graphically using XY-plane:
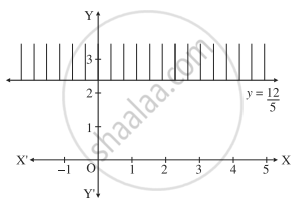
5y - 12 ≥ 0
उत्तर
Consider the line whose equation is 5y - 12 ≥ 0 i.e. y = `12/5`
This represents a line parallel to X-axis passing3through the point `(0, 12/5)`
Draw the line y = `12/5`
To find the solution set, we have to check the position of the origin (0, 0).
When y = 0, 5y - 12 = 5(0) - 12 = - 12 > 0
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line y = `12/5` and the non-origin side of the line which is shaded in the graph.
APPEARS IN
संबंधित प्रश्न
Which of the following statements is correct?
Find the feasible solution of the following inequation:
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
A company manufactures two types of chemicals Aand B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.
| Chemical→ | A | B | Availability |
| Raw Material ↓ | |||
| P | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company gets a maximum profit? Formulate the problem as LPP to maximize profit.
Minimize z = 6x + 2y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
Objective function of LPP is ______.
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
If the corner points of the feasible solution are (0, 0), (3, 0), (2, 1), `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
If the corner points of the feasible solution are (0, 10), (2, 2) and (4, 0), then the point of minimum z = 3x + 2y is ______.
Solve each of the following inequations graphically using XY-plane:
4x - 18 ≥ 0
Solve each of the following inequations graphically using XY-plane:
y ≤ - 3.5
Solve the following LPP:
Maximize z = 4x1 + 3x2 subject to
3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0.
Solve the following LPP:
Maximize z =60x + 50y subject to
x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0.
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
In a cattle breeding firm, it is prescribed that the food ration for one animal must contain 14, 22, and 1 unit of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit weight of these two contains the following amounts of these three nutrients:
| Nutrient\Fodder | Fodder 1 | Fodder2 |
| Nutrient A | 2 | 1 |
| Nutrient B | 2 | 3 |
| Nutrient C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder ₹ 2 per unit. Formulate the L.P.P. to minimize the cost.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. If maximum availability of Machine M1 is 10 hours and that of Machine M2 is 12 hours, then formulate the L.P.P. to maximize the profit.
Choose the correct alternative :
Which of the following is correct?
Choose the correct alternative :
Solution of LPP to minimize z = 2x + 3y st. x ≥ 0, y ≥ 0, 1≤ x + 2y ≤ 10 is
Fill in the blank :
The optimal value of the objective function is attained at the _______ points of feasible region.
Fill in the blank :
“A gorage employs eight men to work in its shownroom and repair shop. The constraints that there must be at least 3 men in showroom and at least 2 men in repair shop are ______ and _______ respectively.
A train carries at least twice as many first class passengers (y) as second class passengers (x) The constraint is given by_______
The point of which the maximum value of z = x + y subject to constraints x + 2y ≤ 70, 2x + y ≤ 90, x ≥ 0, y ≥ 0 is obtained at
Maximize z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
Maximize z = 10x + 25y subject to x + y ≤ 5, 0 ≤ x ≤ 3, 0 ≤ y ≤ 3
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Minimize z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
x − y ≤ 1, x − y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x + y. It is solvable for finding optimum value of z? Justify?
Constraints are always in the form of ______ or ______.
The constraint that in a particular XII class, number of boys (y) are less than number of girls (x) is given by ______
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.
| Requirements | Capacity available per month | ||
| Product A | Product B | ||
| Raw material (kgs) | 60 | 120 | 12000 |
| Machining hours/piece | 8 | 5 | 600 |
| Assembling (man hours) | 3 | 4 | 500 |
Formulate this problem as a linear programming problem to maximize the profit.
Maximize: z = 3x1 + 4x2 subject to 2x1 + x2 ≤ 40, 2x1 + 5x2 ≤ 180, x1, x2 ≥ 0. In the LPP, which one of the following is feasible comer point?
A solution which maximizes or minimizes the given LPP is called
The set of feasible solutions of LPP is a ______.
Shamli wants to invest ₹ 50, 000 in saving certificates and PPF. She wants to invest atleast ₹ 15,000 in saving certificates and at least ₹ 20,000 in PPF. The rate of interest on saving certificates is 8% p.a. and that on PPF is 9% p.a. Formulation of the above problem as LPP to determine maximum yearly income, is ______.
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y Subject to: x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
