Advertisements
Advertisements
Question
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
Solution
Let the number of chairs and tables made by the carpenter be x and y respectively.
The profits are ₹ 140 per chair and ₹ 210 per table.
∴ total profit z = ₹ (140x + 210y)
This is the objective function which is to be maximized. The constraints are as per the following table:
| Chair (x) | Table (y) | Available time (hours) | |
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
From the table, the constraints are
3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60.
The number of chairs and tables cannot be negative.
∴ x ≥ 0, y ≥ 0
Hence, the mathematical formulation of given LPP is:
Maximize z = 140x + 210y, subject to
3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60, x ≥ 0, y ≥ 0
We first draw the lines AB, CD and EF whose equations are 3x + 3y = 36, 5x + 2y = 50 and 2x + 6y = 60 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | 3x + 3y = 36 | A(12,0) | B(0,12) | ≤ | origin side of line AB |
| CD | 5x + 2y = 50 | C(10,0) | D(0,25) | ≤ | origin side of line CD |
| EF | 2x + 6y = 60 | E(30,0) | F(0,10) | ≤ | origin side of line EF |

The feasible region is OCPQFO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (10, 0), P, Q and F (0, 10).
P is the point of intersection of the lines
5x + 2y = 50 … (1)
and 3x + 3y = 36 … (2)
Multiplying equation (1) by 3 and equation (2) by 2, we get
15x + 6y = 150
6x + 6y = 72
On subtracting, we get
9x = 78 ∴ x = `26/3`
Substituting x = `26/3` in (2), we get
`3(26/3) + 3"y" = 36`
∴ 3y = 10
∴ y = `10/3`
∴ P is `(26/3, 10/3)`
Q is the point of intersection of the lines
3x + 3y = 36 ....(2)
and 2x + 6y = 60 ......(3)
Multiplying equation (2) by 2, we get
6x + 6y = 72
Subtracting equation (3) from this equation, we get
4x = 12 ∴ x = 3
Substituting x = 3 in (2), we get
3(3) + 3y = 36
∴ 3y = 27 ∴ y = 9
∴ Q is (3, 9).
Hence, the vertices of the feasible region are O (0, 0),
C(10, 0), P`(26/3, 10/3)`, Q(3,9) and F(0,10)
The values of the objective function z = 140x + 210y at these vertices are
z(O) = 140(0) + 210(0) = 0 + 0 = 0
z(C) = 140(10) + 210(0) = 1400 + 0 = 1400
z(P) = 140`(26/3) + 210(10/3) = (360 + 2100)/3 = 5740/3 = 1913.33`
z(Q) = 140(3) + 210(9) = 420 + 1890 = 2310
z (F) = 140(0) + 210(10) = 0 + 2100 = 2100
∴ z has maximum value 2310 when x = 3 and y = 9.
Hence, the carpenter should make 3 chairs and 9 tables to get the maximum profit of ₹ 2310.
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
A company manufactures two types of chemicals Aand B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.
| Chemical→ | A | B | Availability |
| Raw Material ↓ | |||
| P | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company gets a maximum profit? Formulate the problem as LPP to maximize profit.
If John drives a car at a speed of 60 km/hour, he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 km/hour, the cost of petrol increases ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
Objective function of LPP is ______.
If the corner points of the feasible solution are (0, 0), (3, 0), (2, 1), `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
If the corner points of the feasible solution are (0, 10), (2, 2) and (4, 0), then the point of minimum z = 3x + 2y is ______.
The half-plane represented by 4x + 3y >14 contains the point ______.
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
Solve each of the following inequations graphically using XY-plane:
4x - 18 ≥ 0
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
A firm manufactures two products A and B on which profit earned per unit ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. The product A requires one minute of processing time on M1 and two minutes of processing time on M2, B requires one minute of processing time on M1 and one minute of processing time on M2. Machine M1 is available for use for 450 minutes while M2 is available for 600 minutes during any working day. Find the number of units of product A and B to be manufactured to get the maximum profit.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
Feasible region; the set of points which satify.
Choose the correct alternative :
The corner points of the feasible region are (0, 0), (2, 0), `(12/7, 3/7)` and (0,1) then the point of maximum z = 7x + y
Choose the correct alternative :
The half plane represented by 3x + 2y ≤ 0 constraints the point.
Choose the correct alternative :
The half plane represented by 4x + 3y ≥ 14 contains the point
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Minimize z = 2x + 4y is subjected to 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
State whether the following statement is True or False:
LPP is related to efficient use of limited resources
Constraints are always in the form of ______ or ______.
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.
| Requirements | Capacity available per month | ||
| Product A | Product B | ||
| Raw material (kgs) | 60 | 120 | 12000 |
| Machining hours/piece | 8 | 5 | 600 |
| Assembling (man hours) | 3 | 4 | 500 |
Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
A solution which maximizes or minimizes the given LPP is called
In the given graph the coordinates of M1 are

The maximum value of the objective function Z = 3x + 5y subject to the constraints x ≥ 0, y ≥ 0 and 2x + 5y ≤ 10 is
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
The set of feasible solutions of LPP is a ______.
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
For the following shaded region, the linear constraint are:
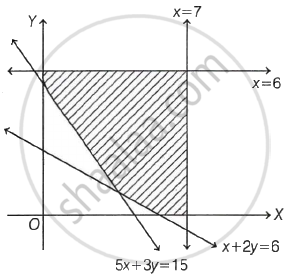
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
Solve the following LPP:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
