Advertisements
Advertisements
Question
The maximum value of the objective function Z = 3x + 5y subject to the constraints x ≥ 0, y ≥ 0 and 2x + 5y ≤ 10 is
Options
6
15
25
31
Solution
15
Explanation:
2x + 5y = 10
| x | 0 | 5 |
| y | 2 | 0 |
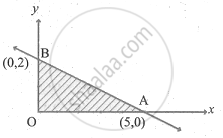
| Corner points | Z = 3x + 5y |
| O(0, 0) | 0 |
| A(5, 0) | 15 |
| B(0, 2) | 12 |
∴ Maximum value is 15
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequations:
x - 2y ≤ 2, x + y ≥ 3, - 2x + y ≤ 4, x ≥ 0, y ≥ 0
If John drives a car at a speed of 60 km/hour, he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 km/hour, the cost of petrol increases ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
The half-plane represented by 4x + 3y >14 contains the point ______.
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
Solve each of the following inequations graphically using XY-plane:
5y - 12 ≥ 0
Solve the following LPP:
Minimize z = 4x + 2y
Subject to 3x + y ≥ 27, x + y ≥ 21, x + 2y ≥ 30, x ≥ 0, y ≥ 0
The feasible region is the set of point which satisfy.
Minimize z = 2x + 4y is subjected to 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
A company produces two types of pens A and B. Pen A is of superior quality and pen B is of lower quality. Profits on pens A and B are ₹ 5 and ₹ 3 per pen respectively. Raw materials required for each pen A is twice as that of pen B. The supply of raw material is sufficient only for 1000 pens per day. Pen A requires a special clip and only 400 such clips are available per day. For pen B, only 700 clips are available per day. Formulate this problem as a linear programming problem.
Solve the following LP.P.
Maximize z = 13x + 9y,
Subject to 3x + 2y ≤ 12,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.
