Advertisements
Advertisements
प्रश्न
The maximum value of the objective function Z = 3x + 5y subject to the constraints x ≥ 0, y ≥ 0 and 2x + 5y ≤ 10 is
विकल्प
6
15
25
31
उत्तर
15
Explanation:
2x + 5y = 10
| x | 0 | 5 |
| y | 2 | 0 |
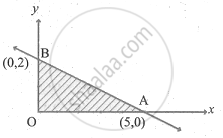
| Corner points | Z = 3x + 5y |
| O(0, 0) | 0 |
| A(5, 0) | 15 |
| B(0, 2) | 12 |
∴ Maximum value is 15
APPEARS IN
संबंधित प्रश्न
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
The maximum value of z = 5x + 3y subject to the constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x, y ≥ 0 is ______.
The half-plane represented by 4x + 3y >14 contains the point ______.
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
Choose the correct alternative :
Solution of LPP to minimize z = 2x + 3y st. x ≥ 0, y ≥ 0, 1≤ x + 2y ≤ 10 is
Fill in the blank :
“A gorage employs eight men to work in its shownroom and repair shop. The constraints that there must be at least 3 men in showroom and at least 2 men in repair shop are ______ and _______ respectively.
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
Solve the following linear programming problems by graphical method.
Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 ≥ 6; x1 + 4x2 ≥ 12 and x1, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
