Advertisements
Advertisements
Question
x − y ≤ 1, x − y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x + y. It is solvable for finding optimum value of z? Justify?
Solution
To draw the feasible region, construct table as follows:
| Inequality | x − y ≥ 1 | x − y ≥ 0 |
| Corresponding equation (of line) | x − y = 1 | x − y = 0 |
| Intersection of line with X-axis | (1, 0) | (0, 0) |
| Intersection of line with Y-axis | (0, −1) | (0, 0) |
| Region | Origin Side | Test point: (1, 0) 1 − 0 ≥ 0, which is true. The side containing (1, 0) |
x ≥ 0, y ≥ 0 represent 1st quadrant.
Here, the feasible region is unbounded.
So, the objective function does not have finite maximum value, i.e. the value of objective function, increases indefinitely and hence the L.P.P has unbounded solution.
∴ The optimal solution does not exist.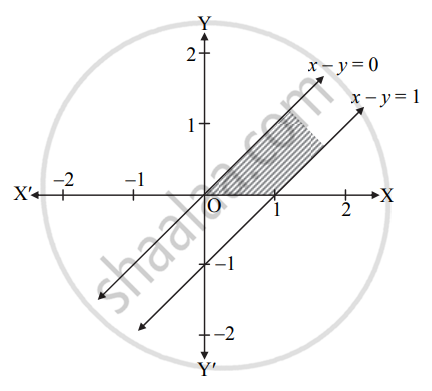
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Find the feasible solution of the following inequation:
3x + 4y ≥ 12, 4x + 7y ≤ 28, y ≥ 1, x ≥ 0.
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14. 22 and 1 units of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients:
| Fodder → | Fodder 1 | Fodder 2 |
| Nutrient ↓ | ||
| Nutrients A | 2 | 1 |
| Nutrients B | 2 | 3 |
| Nutrients C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 ₹ 2. Formulate the LPP to minimize the cost.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 in magazines A and B per copy. These are processed on three Machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II, and 2 hours on machine III. Magazine B requires 3 hours on machine I, 2 hours on machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, and 60 hours per week respectively. Formulate the LPP to determine weekly production of magazines A and B, so that the total profit is maximum.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
Solution of LPP to minimize z = 2x + 3y, such that x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is ______.
The half-plane represented by 4x + 3y >14 contains the point ______.
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
Solve each of the following inequations graphically using XY-plane:
4x - 18 ≥ 0
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
Solve the following LPP:
Maximize z = 4x1 + 3x2 subject to
3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0.
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
A company produces mixers and food processors. Profit on selling one mixer and one food processor is Rs 2,000 and Rs 3,000 respectively. Both the products are processed through three machines A, B, C. The time required in hours for each product and total time available in hours per week on each machine arc as follows:
| Machine | Mixer | Food Processor | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced in order to maximize the profit?
Choose the correct alternative :
Of all the points of the feasible region the optimal value of z is obtained at a point
Choose the correct alternative :
Feasible region; the set of points which satify.
Choose the correct alternative :
The half plane represented by 4x + 3y ≥ 14 contains the point
Fill in the blank :
The optimal value of the objective function is attained at the _______ points of feasible region.
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
Maximize z = 5x + 2y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Minimize z = 2x + 4y is subjected to 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
Constraints are always in the form of ______ or ______.
A company produces two types of pens A and B. Pen A is of superior quality and pen B is of lower quality. Profits on pens A and B are ₹ 5 and ₹ 3 per pen respectively. Raw materials required for each pen A is twice as that of pen B. The supply of raw material is sufficient only for 1000 pens per day. Pen A requires a special clip and only 400 such clips are available per day. For pen B, only 700 clips are available per day. Formulate this problem as a linear programming problem.
Maximize: z = 3x1 + 4x2 subject to 2x1 + x2 ≤ 40, 2x1 + 5x2 ≤ 180, x1, x2 ≥ 0. In the LPP, which one of the following is feasible comer point?
A firm manufactures pills in two sizes A and B. Size A contains 2 mgs of aspirin, 5 mgs of bicarbonate and 1 mg of codeine. Size B contains 1 mg. of aspirin, 8 mgs. of bicarbonate and 6 mgs. of codeine. It is found by users that it requires at least 12 mgs. of aspirin, 74 mgs. of bicarbonate and 24 mgs. of codeine for providing immediate relief. It is required to determine the least number of pills a patient should take to get immediate relief. Formulate the problem as a standard LLP.
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
The maximum value of Z = 3x + 5y, subject to 3x + 2y ≤ 18, x ≤ a, y ≤ 6, x, y ≥ 0 is ______.
Which of the following can be considered as the objective function of a linear programming problem?
The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is ______
Solve the following LP.P.
Maximize z = 13x + 9y,
Subject to 3x + 2y ≤ 12,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.
The optimal value of the objective function is attained at the ______ of feasible region.
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
Find graphical solution for the following system of linear in equation:
x + 2y ≥ 4, 2x - y ≤ 6
